Kombinatorik
Hej! Har lite frågor gällande kombinatorik är lite förvirrad gällande vad som är vad.
1. Hur avgöra man i en uppgift om det handlar om permutationer eller kombinationer & hur skiljer man på de?
Min tolkning: som jag förstått det så spelar ordningen roll för permutationer men inte för kombinationer. För permutationer gäller ju k! men förstår inte varför man ska ta bort.
Ex. När man väljer 3 personer i en grupp av 5. För permution blir det ju 5!= 5•4•3•2•1. Varför ska man sen dividera?
2. Vad är skillnaden mellan multiplplikattions principen & permutationer?
Att välja 3 personer från 5 blir 5*4*3 om du räknar permutationer.
Precis som du säger kommer ordningen spela roll. Har vi A-E att välja mellan kommer t.ex A,B;C och B,A,C vara olika permutationer, men samma kombination.
För att bestämma antalet kombinationer tar vi helt enkelt antalet permutationer och dividerar med antalet sätt att permutera varje val så att samma element ingår. Det finns 3! sätt att ordna 3 element på, därmed blir antalet permutationer 5*4*3/3!
I fråga 1: förstår jag inte varför man sen ska dividera med 3!= dvs 6 för att få antal kombinationer. Blir det alltså 5!/3!= 60/6=10
Ja det blir det.
Tänk så här:
Av de 60 valen så innehåller flera samma element men i olika ordning.
T.ex. om vi valt ABC så finns också ytterligare 5 utfall med ABC men i annan ordning vi har alltså räknat varje kombination 6 gånger och därför dividerar vi med 6.
Multiplikationsprincipen känner jag inte till, i alla fall inte under det namnet.
Hänger fortfarande inte riktigt med blir ju enligt denna om det är ordat urval (5!/(5-3!))= 5!/2! = 60.
5 då vi har 5 möjliga personer. Och 3 st ska ingår i varje grupp dvs 5 möjliga val men enbart 3 st som ska göras.
förstår liksom inte hur man kopplas ihop det:( Dividerar man alltid med fakulutet för de val som gör? När man räknat ut på den vanligasättet för ordnat val? ?
Dvs om ex vi hade haft 12 bollar som ska grupperas i 5 grupper.
antal val: 5 (k)
möjliga val: 12 (n)
får vi först 12!/(12-5!)= 12!/7!
då ska man sen dividera detta med 7!?
när jag från början ens försöker komma fram till 60 enlig formeln får jag fel också
Alltså i exemplet innan
då vi har totalt 5 personer= n ( 5 objekt)
med 3 val= k
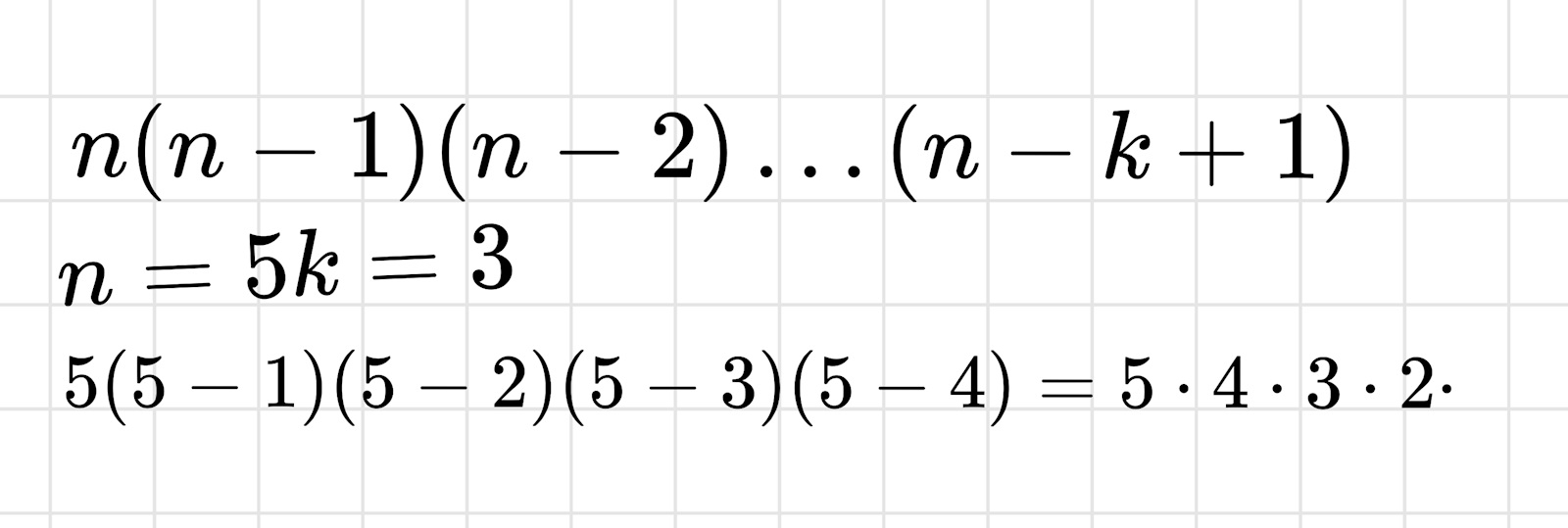
sedan försökte jag skriva om det igen men blir helt konstigt

eller är det för att det istället ska skrivas som (n-k)+ 1 så här..? Dvs man räknar alltid n-k för sen adderar 1?

Hej,
När vi gör ett ordnat urval av från objekt, använder vi multiplikationsprincipen som du nämnde, som säger att om vi utföra en procedur (här att ordnat välja 3 personer från 5 personer) i flera steg, där det ena kan utföras på sätt, det andra på sätt osv, så får vi antalet sätt att utföra proceduren på genom att multiplicera ihop dessa. Här så kan vi välja den första personen på sätt, den andra på sätt och den tredje på sätt. Så antalet sätt att välja alla tre blir som du skrev.
I det generella fallet när vi ordnat ska välja saker från saker blir det alltså
Förlänger vi med i täljare och nämnare får vi
Om vi nu vill ha antalet oordnade urval (kombinationer) så kan vi dela bort antalet sätt att ordna saker nämligen och få
Men hur vet man hur många fakulteter man ska dividera med? Ex om de är 4 st bokstäver istäklet blir det 4! Att dividera med då? Eftersom ytterligare ett val ska göras?
Tänker du på formeln för antal permutationer eller antal kombinationer nu?
Om vi ska ordnat välja (permutera) 4 bokstäver av 5 blir det .
Hej tänker både och:)
Varför väljer man att förlänga i nämnaren?
Det blir ett lite mer kompakt sätt att skriva det på tänker jag. Om vi till exempel ska välja 40 saker från 100 så blir det enklare/mer kompakt att skriva
än .
I fallet där vi oordnat väljer 4 saker från 5 saker delar vi bort så det blir
.
Man kan även tolka det som att det finns 5 sätt att välja vilken sak vi inte väljer.
Tvekade lite om jag skulle komplicera tillvaron med fler alternativ men det är ju universtetsnivå så:
Jag vill helst skriva formeln som för att välja m srtycken av m+n stycken som (m+n)!/m!n! dels för att det framhäver symmetrin - i vårt exempel: Att välja 3 av 5 är samma som att välja bort 2 av 5
och dels för att det leder vidare till att välja till flera högar med vardera i,j,k... enheter blir polynomialkoefficienten
(i+j+k+l+...)! / i!j!k!l!...
Hej! Det är föredande mattekurs efter matte 3 på gymnasie nivå
Aha så i vl har du skrivi på n-k+1 formeln med hl n!/n-k formen? Om man skriver på vl formeln är det alltid att man fortsätter skriva ut till och med 1 mindre en över det k- värdet. Dvs i fallet ovan k+1= 3+1 = 4
Varför skriver du 4!•1! Dvs med 1?
Så när ordningenen inte spelar roll tar man alltså k! värdet genom det man fått när man tidigare räknat n!/(n-k!)
Finns det något mer generelmt kompakt sätt att skriva detta på?
Har jag tänkt rätt här?
K- Antal val 3 st bland 5
1a → 5 sätt (n)
2:a → 4 sätt(n-1)
3:a → 3 sätt (n-k+1)
Ordnat urval (om ordning spelar roll)
Välj: 3 st (k)
- k= antal val (3 st personer)
Bland: 5 st (n)
-n= 5 totala personer grupper ska väljas
Formel: n(n-1)(n-2)… (n-k+1) alternativ n!/(n-k)!
k= personer ska väljas (3 st)
n= tillgängliga objekt/ personer (5 st)
Formel: Oordnat välja k objekt från n element
Formel
n(n-1)(n-2)… (n-k+1)/k!
Varje kombination: 3! permutationer dvs svaret som man får i det ornade falet divideras med k! (3!=3•2•1 dividera med 6)
Varje kombination: svarar för 6 permutationer i fallet (3!)
60/6= 10
Formel: 5!/(5-3)!= 60 (ordning spelar roll)
Ordningen spelar inte roll i detta fall: vilket gör att man dividerar med 3! (Dvs antal personer): 60/3!=10
Personer: P1-P5

Varning för en viss begreppsförvirring.
Under ordnat urval kallas plötsligt formeln för oordnat urval (men rätt formel för ordnat urval, åtminstone om man menar urval där ordningen spelar roll)
och formeln som kallas ordnat urval ger antalet för ett urval där ordningen inte spelar någon roll.
Det naturligtvis tillåtet att kalla ett urval där ordningen inte spelar någon roll för ordnat urval men inte underlättar det tänkandet.



