Kluringar i HP-tappning

Högskolenivå ?

larsolof skrev :

Högskolenivå ?

Den matematik som brukar behövas på högskoleprovet är vanligen första-andra året på gymnasiet.

$\sqrt{\frac{64}{81}}=\sqrt{64}/\sqrt{81}=8/9$

Snyggt!

XYZ: Ralf samlar på reklampennor, och skickar därför ut mail till ett antal olika företag och frågar om de kan tänka sig att skicka en penna med företagets logga på. Några företag hakar på, och spridningen fördubblas varje dag. Fem pennor kommer på tisdagen. Hur många pennor har det totalt kommit på posten när fredagen är slut?

A: 90 pennor
B: 75 pennor
C: 60 pennor
D: 40 pennor

Tis (5) ons(10) tor(20) fre(40) = 75 

Det är ett bra sätt att lösa uppgiften på. Det går också att tänka på följande sätt:

En dubblering av ett tal som slutar på fem (X5, XX5, XXX...X5, osv) ger ett tal som slutar på noll. En dubblering av ett tal som slutar på noll (X0, XX0, XXX...X0) ger också ett tal som slutar på noll. Vi får alltså aldrig tillbaka någon femma efter tisdagen. Det enda nollskilda entalet i summan är då en femma. Eftersom endast ett av alternativen slutar på fem kan vi direkt sluta oss till att svaret måste vara B, 75. 

NOG: Cilla ska baka muffins. Receptet hon hittat ger femton muffins, och består av följande ingredienser:

2 ägg
3 dl socker
1 tsk vaniljsocker
2 tsk bakpulver
1 dl mjölk
3 dl mjöl

Hur många muffins har Cilla bakat?

(1): Om mängden socker minskar med 6 dl, minskar mängden bakpulver med 4 tsk.

(2): Om mängden mjölk dubbleras ökar antalet muffins med 30.

Tillräcklig information för lösningen erhålls:

A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) separat
E: ej genom de båda påståendena 

B)

$$\begin{gathered} Deciliter mjölk 1 2 3 4 \\ Antal muffins 15 30 45 60 \\ Måste vara 30 muffins (2dl mjölk) för o få +30 muffins med dubbla antal decilitermjölk\left(4dl\right) \end{gathered}$$

Intressant lösningsmetod. En annan metod är följande:

(1): Ger information om förhållandet mellan socker och bakpulver. Det har vi redan från receptet. Oavsett hur många satser Cilla gör kommer en minskning med 6 dl mjölk alltid att innebära en minskning med 4 tsk. bakpulver. (1) bidrar alltså inte med någon ny information.

(2): Detta påstående ger oss information om mängden mjölk i förhållande till mängden muffins. Det är däremot mer intressant. En ökning med 30 muffins innebär en ökning med två satser. En dubblering av mängden mjölk innebär alltså att mängden muffins ökar med 2 satser. Varje muffinsats  innehåller 1 dl mjölk. Vi kan då räkna ut vad 2 dl mjölk innebär, och därmed hur många muffins hon bakar. 

Svar: B, i (2) men ej i (1).

NOG: Två räta linjer dras på ett papper. En tredje rät linje skär de två räta linjerna.

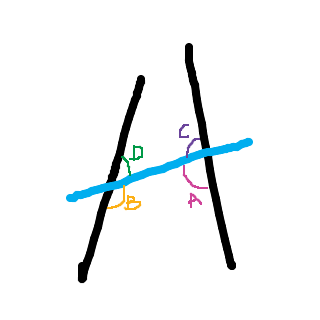Är linjerna parallella med varandra?

(1): Vinkeln C är inte rät.

(2): Vinklarna $A+C$ och $B+D$ är båda lika med 180 grader.

Tillräcklig information för lösningen erhålls:

A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2) 
D: i (1) och (2) separat
E: ej genom de båda påståendena 

E, det finns ej tillräcklig info för o räkna ut det.

Jag drar en bump av denna tråd, en söndag som denna!

Aufzen: Det stämmer, men hur kom du fram till ditt svar?

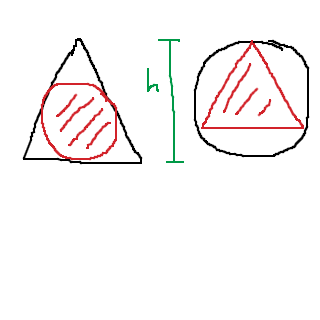
En cirkel är inskriven i en liksidig triangel i bild ett, medan en triangel är inskriven i en cirkel i bild två. Den stora triangelns och den stora cirkelns höjd är lika stora. Vilken area är störst?

I: Den lilla cirkelns area
II: Den lilla triangelns area

A: I är större än II
B: II är större än I
C: I är lika med II
D: Tillräcklig information saknas

Svar: A         $\left( I\approx 0,349·h^2 II\approx 0,325·h^2 \right)$

Smutstvätt skrev :

---

En cirkel är inskriven i en liksidig triangel i bild ett, medan en triangel är inskriven i en cirkel i bild två. Den stora triangelns och den stora cirkelns höjd är lika stora. Vilken area är störst?

I: Den lilla cirkelns area
II: Den lilla triangelns area

A: I är större än II
B: II är större än I
C: I är lika med II
D: Tillräcklig information saknas

Hur har larosof löst?

En halv liksidig triangel har vinklarna  30  60  90  grader och sidlängderna
förhåller sig som  1  2   $\sqrt{3}$
halva basen = AM = $\frac{h}{\sqrt{3}}$                                                FGH  delas  i  6 trianglar, alla  30-60-90 grader
ACM är likformig med AOM  (båda 30-60-90)            HC = $\frac{h}{2}$       lilla kateten = $\frac{h}{4}$
cirkelradien = OM = $\frac{h}{\sqrt{3}·\sqrt{3}}=\frac{h}{3}$                                stora kateten = $\frac{h·\sqrt{3}}{4}$
area = $\frac{h}{3}·\frac{h}{3}·\mathrm{\pi }=\frac{\mathrm{\pi }}{9}·{\mathrm{h}}^2 \approx 0,349·{\mathrm{h}}^2$     area =  $\frac{h}{4}·\frac{h·\sqrt{3}}{4}·\frac{1}{2}·6 = \frac{3·\sqrt{3}}{16}·h^2 \approx 0,325·h^2$

Jag hade glömt att premunera, som är synd för att jag skulle ha kunnat sova på det

• halva basen = AM (ok) = $\frac{h}{\sqrt{3}}$ (inte ok!)

Jag har nog haft en överkokat hjärna i matte 3 när vi gick igenom liksidighet, så jag förståd inte den roligt permutation du har gjort just nu. 

• cirkelradien = OM = $\frac{h}{\sqrt{3} \cdot \sqrt{3}}$

Jag fattar att du fortsätter med samma principen, men eftersom jag har nu missat en viktig avsnitt... förstår jag inte varför Cersei Lannister pratar nu med Drakdrottningen om man säger så. Vad är det som har hänt?

Trianglet nu:

• att HC är $\frac{h}{2}$ är jag med, men den lilla kateten $\frac{h}{4}$? Varför? 
• den stora kateten = $\frac{h \cdot \sqrt{3}}{4}$. Vem pratar vi om? Och varför blir det så?

En liksidig triangel har 3 lika långa sidor, och tre lika stora vinklar, 60-60-60.
Om man delar den med ett snitt från toppen till mitt på basen ( C till M  i figuren ovan)
får man en rätvinklig triangel ACM med vinklarna 30-60-90 grader.

Om hypotenusan AC är 2 l.e. så är kateten AM 1 l.e.  kateten CM = $\sqrt{3}$
Bevis:  Pythagoras sats:   $2^2 = 1^2 + {\mathrm{h}}^2$     $\Rightarrow {\mathrm{h}}^2 = 3 \Rightarrow \mathrm{h} = \sqrt{3}$

Så sidorna i en rätvinklig triangel med vinklarna 30-60-90 grader
förhåller sig alltid som        2      1      $\sqrt{3}$   (hypotenusa katet katet)

Därför kan de även vara    $2\mathrm{h}$    $1\mathrm{h}$   $\mathrm{h}\sqrt{3}$

                              eller     $\frac{2\mathrm{h}}{\sqrt{3}}$   $\frac{1\mathrm{h}}{\sqrt{3}}$  $\frac{\mathrm{h}\sqrt{3}}{\sqrt{3}}$

                               dvs      $\frac{2\mathrm{h}}{\sqrt{3}}$   $\frac{\mathrm{h}}{\sqrt{3}}$    $\mathrm{h}$    och detta är längderna i figuren 

                                            AC    AM    CM

Nu känner vi alla sidor i ACM, och ACM är likformig  med AOM.
AM är gemensam för båda. Då kan man räkna ut OM så här

$\frac{\mathrm{AM}}{\mathrm{CM}} =\hspace{0.17em}\frac{\mathrm{OM}}{\mathrm{AM}} \Rightarrow \frac{{\displaystyle \frac{\mathrm{h}}{\sqrt{3}}}}{\mathrm{h}} = \frac{\mathrm{OM}}{{\displaystyle \frac{\mathrm{h}}{\sqrt{3}}}} = \frac{\mathrm{h}}{3}$ 

Triangeln nu:

Alla 6 småtrianglarna är ju likformiga, så räkna på en av dem t.ex. den översta högra.
Den har hypotenusan HC = $\frac{\mathrm{h}}{2}$       
Denna lilla triangel har också två kateter, de jag kallar "lilla kateten" och "stora kateten".
Eftersom triangeln är en rätvinklig triangel med vinklarna 30-60-90 grader
så förhåller sig sidorna som  $2 1 \sqrt{3}$      (som visats ovan)

Då  HC = $\frac{\mathrm{h}}{2}$   så  är "lilla kateten" = $\frac{\mathrm{h}}{4}$    och   "stora kateten" =  $\frac{\mathrm{h}\sqrt{3}}{4}$

Återstår att räkna ut totalarean:   "lilla kateten"   x   "stora kateten"   x   $\frac{1}{2}$   x   6

Tack, detta var den bäst avsnitt recap nånsin! Tack o lov var jag bekant med 30° 60° och 90° regel...

Här:

om $HC=\frac{h}{2}$ det är bara att multiplicera med $\sqrt{3}$ och dividera med $2$ för att få den "stora kateten"? Jag blev lite förvirrad i början varför det är delat med 4?

Detta var oerhört intressant, jag tror jag ska även kopiera det nånståns på anteckningsblock. Finns det nåt snabbare sätt att inse detta på HP? 

Finns det nåt regel att om en cirkel är inskriven i en triangel då är diameter $\frac{2}{3}$ av höjden? Eller ännu bättre, kan vi deducera detta redan igenom att jämföra höjden av de 2 liksidiga trianglar? Typ: att cirkeln inskriven i en triangel med höjden h har större area en triangel med höjden $\frac{3}{4}$ av h?

EDIT: nu har jag nog förstörd kluring tråd med mina dumma frågor, säg till om jag får öppna en dottertråd för utvecklingar.