Kedjeregeln förklaring
Hej,
Jag tycker det bara konstateras att kedjeregeln är korrekt utan att visa varför/hur. Man multiplicerar derivatan av inre och yttre funktionen exempelvis, okej, varför gör man det?
Ser exempel då med Leibniz notation där man visar att om vi betraktar det här som ett bråk så försvinner 'du' när vi multiplicerar ihop 'bråken' och kvar får vi då Derivatan av den sammansatta funktionen. Jag vet inte, tycker inte att det säger någonting överhuvudtaget egentligen.
Tänkte.. går det att förklara den intuitivt med ett enkelt exempel så man kan greppa den lite bättre? Undrar också om jag kan, typ, göra grafen för en inre funktion, kolla derivatan, och ta med värdena där till den yttre funktionen osv och liksom följa 'kedjan' och se att, okej, det här är vad som händer?
här finns ett bevis för kedjeregeln
Hej Ture,
Tack! Men jag förstår inte bevis. Exempelvis:
"Hur skriver man om detta till produkten i formeln? Första steget är att förlänga bråket med ett lämpligt uttryck för att få ett gränsvärde av en produkt. Då kan man dela upp gränsvärdet som produkten av två andra gränsvärden, som båda beskriver derivator." - Okej, varför vill vi göra det? Varför vill vi ha en produkt av två gränsvärden?
¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤
Har funderat lite och jag tänker någonting sånt här:
Om vi har yttre funktionen f(g(x)) = Q
Och inre funktionen g(x), med variabeln x.
Derivatan av en sammansatt funktion frågar: hur förhåller sig förändringshastigheten av hela funktionen med avseende på variabeln x?
Om variabeln x är en cykel.
Och g(x) u är en bil.
Och Q är ett tåg.
Vi vill veta hur tåget förhåller sig till cykeln.
¤¤
Bilen går 6 gånger så snabbt som cykeln. Så sträckan som bilen förflyttar sig på förändras 6 gånger snabbare än cykeln.
Nu vill vi jämföra tåget och bilen. Tågets hastighet jämförs endast med bilen.
Tåget går 3 gånger snabbare än bilen.
¤¤¤¤¤
Skulle vi enbart jämföra tåget med bilen här, så är vi endast intresserade av derivatan av Q med avseende på g(x), inte Q med avseende på x. Det vill säga förändringshastigheten är då 3x.
Men nu är vi intresserade av hur tåget förhåller sig till cykeln, och cykeln påverkar i sin tur bilen, alltså är vi intresserade av hur sammansatta funktionen Q förhåller sig till cykeln.
Tåget Går 3 gånger snabbare än bilen, bilen går 6 gånger snabbare än cykeln.
Därför har vi att förändringshastigheten av Tåget med avseende på cykel = dtåg/dbil * dbil/dcykel.
Eller 3*6 = 12.
Jag tycker denna är tydligare;
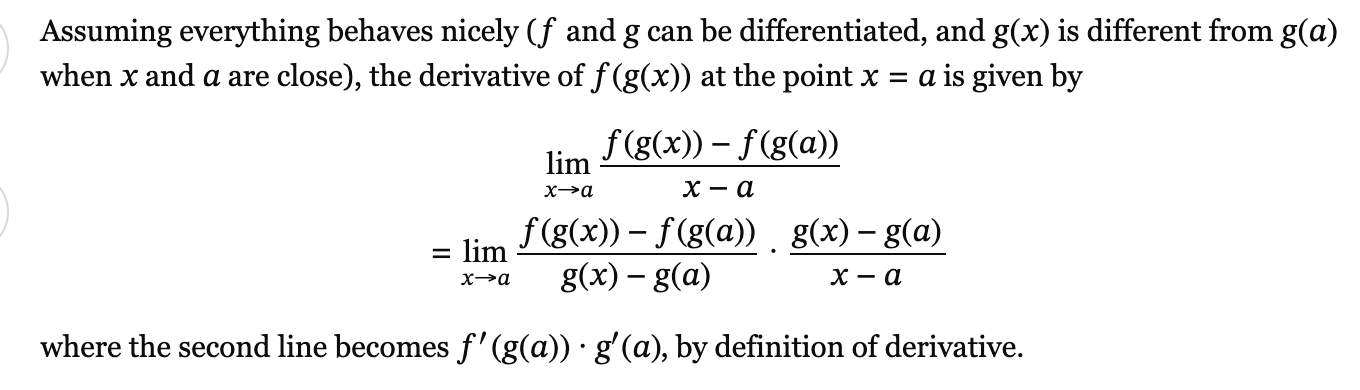
https://math.stackexchange.com/questions/1180686/how-to-prove-the-chain-rule
Angående Tures länk:
Jag vet inte varifrån jag har fått detta men jag har för mig att beviset på mathleaks inte är allmänt.
Och om man jobbar i talsystem med bra infinitesimaler så är kedjeregeln trivialt sann. Säg att vi har y=f(g(x))). Då har vi trivialt att dy/dx = df/dx = df/dg * dg/dx
dg:na ”tar ut varandra”. Om man också har tillgång till std-funktionen kan man göra det lite mer rigoröst.
Har jag rätt i mitt resonemang i inlägg #3?
Tillägg: 27 dec 2024 19:41
Undrar lite över vad det är ni förstår som inte jag gör i dom här bevisen, vad ni ser för någonting. Förklarar ingenting för mig alls, märkligt.
Tillägg: 27 dec 2024 19:41
Undrar lite över vad det är ni förstår som inte jag gör i dom här bevisen, vad ni ser för någonting. Förklarar ingenting för mig alls, märkligt.
Kanske denna video kan ge en liten intuition om kedjeregeln?
AlexMu skrev:Tillägg: 27 dec 2024 19:41
Undrar lite över vad det är ni förstår som inte jag gör i dom här bevisen, vad ni ser för någonting. Förklarar ingenting för mig alls, märkligt.
Kanske denna video kan ge en liten intuition om kedjeregeln?
Ja, brukar kolla på hans material. Det är svårt att förstå ändå. Han förklarar ofta det matematiska med matematik, men det är ofta precis det jag inte begriper. Tycker mycket om betterexplained.com också, han försöker förklara koncept från många olika perspektiv, men brukar som första steg förklara det mer metaforiskt med hjälp av alla möjliga liknelser. Väldigt lekfullt och sådär.
Jag är ganska säker på att jag förstår kedjeregeln nu, i varje fall. Är inte alls med på bevisen dock hur man kommer fram till att man ska multiplicera derivatorna. Får väl leva med det, jag vet inte. Har konsumerat ganska mycket material nu, men det går inte.
Jag är lite fundersam till vad du menar med att du inte ”förstår” bevisen som hänvisats till här. Det som gör ett bevis felaktigt är att något steg är logiskt felaktigt eller olagligt, t.ex. en olaglig aritmetisk operation.
Hittar du något sådant i något av bevisen, eller vad är det du hakar upp dig på?
Skulle nog säga att jag klarar ofta inte av att följa logiken. Hänger inte med, helt enkelt. Jag fattar inte. Kan inte riktigt förklara det.
Lyckas inte översätta det matematiska språket till information som jag kan bearbeta, riktigt. Det lutar starkt åt jag inte inte kan bättre.
Specifikt i det här fallet förstår jag inte varför man väljer att multiplicera med g(x) - g(a)/x-a. Kan inte se någon logisk anledning att utföra den operationen. Om jag nu inte översätter regeln till någon form av historia där jag kan förhålla mig till det, då är det ganska självklart att man behöver multiplicera med derivatan för den inre funktionen för att få den totala förändringen.
Anledningen till att man väljer att multiplicera med det är för att man inser att det leder till en form där man kan tillämpa derivatans definition två gånger.
Men ofta spelar det inte så stor roll ”varför” man väljer att utföra ett visst steg, såvida du inte vill konstruera beviset själv. Det som är viktigast är att det _inte är olagligt_. Om du kan ta dig igenom hela beviset och kan acceptera varje steg av beviset - oavsett om du förstår _varför_ det utförs - förstår du också beviset.
Jo, och då måste man först inse att det gör det, och vidare också inse att det nog behövs ett steg till i någon form där överhuvudtaget.
Är lite problematiskt envis och måste förstå allting så långt jag kan intuitivt, som leder till problem när jag inte klarar det på en nivå som känns tillfredsställande. Vill då inte gå vidare och fastnar i ändlösa funderingar.
Men förstår vad du menar. Det klarar jag nog av. Fast jag vill gärna vara/bli mycket bättre och kunna konstruera sådant själv, och tänker att då måste man kunna förstå vad man håller på med på en lite djupare nivå.
Får trassla mig vidare så får man se vad det blir 🙂




