Kaströrelser

Någon vänlig själ som kan hjälpa mig med denna uppgift?

Ett flygplan flyger horisontellt med hastigheten 180 km/h på höjden 45 m ovanför marken. Från planets undersida lösgörs ett tungt oömt föremål i det ögonblick det befinner sig rakt ovanför en viss punkt P på marken.

Hur långt från P slår föremålet ner? Marken är horisontell. Luftmotståndet försummas.

Förstår att formlerna x=v0x och y=v0y*t-(gt^2)/2 används och att v0x=180km/h=50m/s, v0y=0m/s

men fastnar på att lösa ut t här: 45=(-9.82*t^2)/2 --> t^2=90/-9.82 --> roten ur 90/-9.82 går inte eftersom nämnaren är negativ? Hur kan jag få ut högra sidan utan ett negativt tal?

Du tänker mycket rätt. Det som du gör fel på är vad du definierar vara positiv riktning i y-led. Rörelseekvationen i y-led är

$s_{y} = v_{0 y} \cdot t + \frac{a_{y} \cdot t^{2}}{2}$

dvs du har tre storheter (förutom tiden). Sträcka, hastighet och acceleration i y-led, som du _måste_ vara konsekvent när du beskriver vad som är positiv och negativ riktning. $v_{0 y}$ är noll, eftersom föremålet lösgörs utan initialhastighet i y-led. Där har du gjort rätt. Problemet är att du använder accelerationen $- 9.82 m / s^{2}$ , dvs negativ acceleration nedåt (tyngdaccelerationen pekar mot jordytan). Du får såklart lägga koordinatsystemets axlar hur du vill, men isåfall måste du ange sträckan i samma koordinatsystem med negativ riktning nedåt, dvs $- 45 m$ .

Hänger du med?

Ja jag tror det. Gäller den formeln du skrev om jag anger y sträckan neråt som positiv? Nu hänger jag med, tack! Har också hört fler som velat rita ett koordinatsystem för föremålets rörelse, har ingen aning om hur jag ritar den. Hur ska jag se sträckan i ett Vy, Vx system?

Ja, jag hade nog själv valt att beskriva accelerationen och sträckan (läget) som positivt nedåt, eftersom det hade känts mest intuitivt för mig. Men det spelar ju ingen roll vad man väljer, bara man är konsekvent med alla storheter. Jag misstänker att anledningen till att du valde att beskriva tyngdaccelerationen som negativ är för att du har kanske jobbat med någon kaströrelseuppgift där man har kastat ett föremål uppåt, och låtit det falla ner. I ett sådant fall så kan det ju vara mest intuitivt att välja positiv riktning uppåt, så att man har positiv utgångshastighet, varpå hastigheten byter tecken och blir negativ då föremålet vänder och börjar falla nedåt.

Bra fråga hur man ska se på sträckan!

Vid rörelse med konstant acceleration längs en rät linje så lär man sig ju formeln $s = v_{0} t + \frac{a t^{2}}{2}$ (eller kanske $x = v_{0} t + \frac{a t^{2}}{2}$ så att relationen med koordinatsystemet blir tydligare) på gymnasiet.

På gymnasiet lär man sig också att hastigheten och accelerationen är vektorer med storlek och riktning. För rörelseekvationen ovan gäller då att man måste definiera vad som är positiv riktning för hastigheten och accelerationen. Och för sträckan, eller ”läget” för föremålet man räknar på, måste man dessutom sätta ett origo, dvs läget noll, vilket brukar vara mest intuitivt att sätta vid tiden t=0. Det är detta som är ditt koordinatsystem (koordinataxel). Du inser ju att beroende på vilket tecken du har för hastigheten och accelerationen för ett föremål, så kommer du att få helt olika värden på läget vid tiden t för föremålet. Ett negativt läge är lägen som befinner sig på den negativa delen i ditt koordinatsystem.

tack så mycket! Förstår uppgiften nu men lite krångel med att rita koordinatsystemet :( Gör man systemet med Vy och Vx kan man ju inte se föremålets sträcka, alltså hur den rör sig neråt? Och om Vy = 0 blir då föremålet i koordinatsystemet bara en punkt där Vx = 50m/s?

Då försöker vi reda ut krånglet. Jag gör två exempel, samma uppgift, två olika koordinatsystem:

1. Rita koordinataxlar i x- och y-led för läget, positiv x-riktning åt planets rörelseriktning, positiv y-riktning nedåt. Origo där man släpper föremålet.

$a_{y} = 9.82 m / s^{2}$ , alltså positiv eftersom accelerationen pekar i samma riktning som positiv y-axel. $v_{x} = 50 m / s$ , alltså positiv eftersom hastigheten pekar i samma riktning som positiv x-axel.

Marknivån ligger på $y = 45 m$ i koordinatsystemet eftersom marknivån skär positiv y-axel. Punkten P har koordinater $(0, 45 m)$

Rörelseekvationen i y-led blir då $y = \frac{a_{y} t^{2}}{2} \Rightarrow 45 = \frac{9.82 t^{2}}{2} \Rightarrow t = . . .$

Rörelseekvationen i x-led blir då $x = v_{x} t \Rightarrow x = 50 t$

och den beräknade x-koordinaten för nedslaget blir positiv, dvs en punkt framför flygplanet.

2. Men man hade lika gärna kunnat lägga koordinataxlarna åt andra hållet.

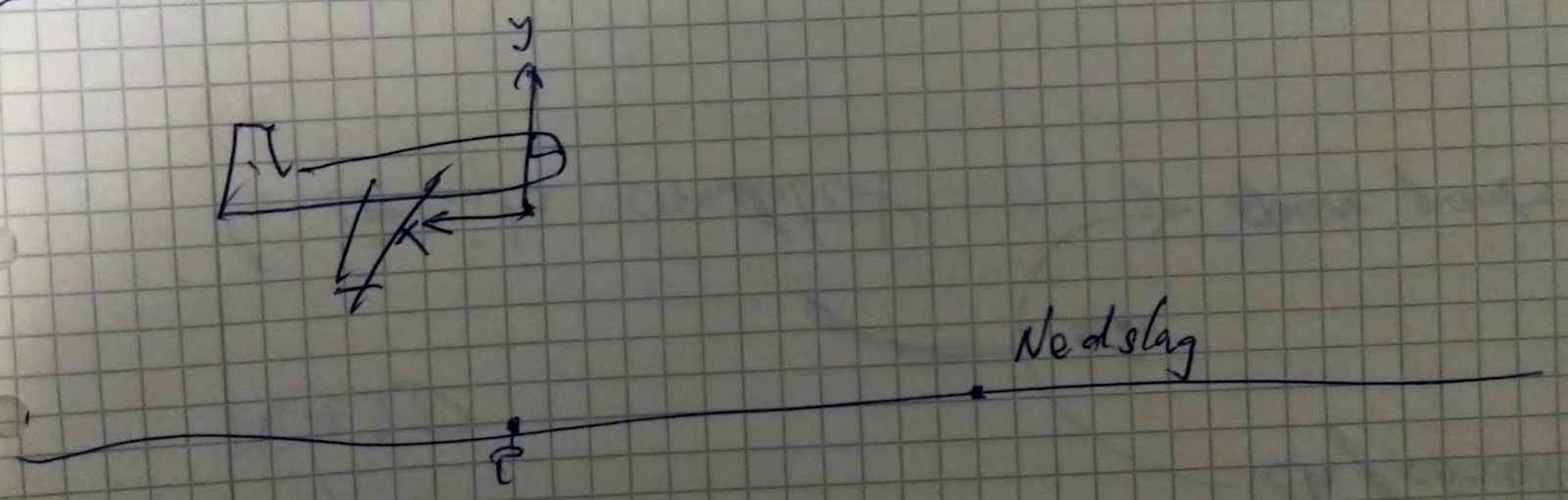
$a_{y} = - 9.82 m / s^{2}$ , alltså negativ eftersom accelerationen pekar i motsatt riktning som positiv y-axel

$v_{x} = - 50 m / s$ , alltså negativ eftersom hastigheten pekar i motsatt riktning som positiv x-axel

Marknivån ligger på $y = - 45 m$ i koordinatsystemet eftersom marknivån skär negativ y-axel. Punkten P har koordinater $(0, - 45 m)$

Rörelseekvationen i y-led blir då $y = \frac{a_{y} t^{2}}{2} \Rightarrow - 45 = \frac{- 9.82 t^{2}}{2} \Rightarrow t = . . .$

Rörelseekvationen i x-led blir då $x = v_{x} t \Rightarrow x = - 50 t$

och den beräknade x-koordinaten för nedslaget blir negativ, dvs en punkt framför flygplanet.

tack så mycket! förstår det nu speciellt med första bilden du ritade :)

Grejt!

Svara

Visa senaste svar