Kan uttrycket förenklas till
Hej!
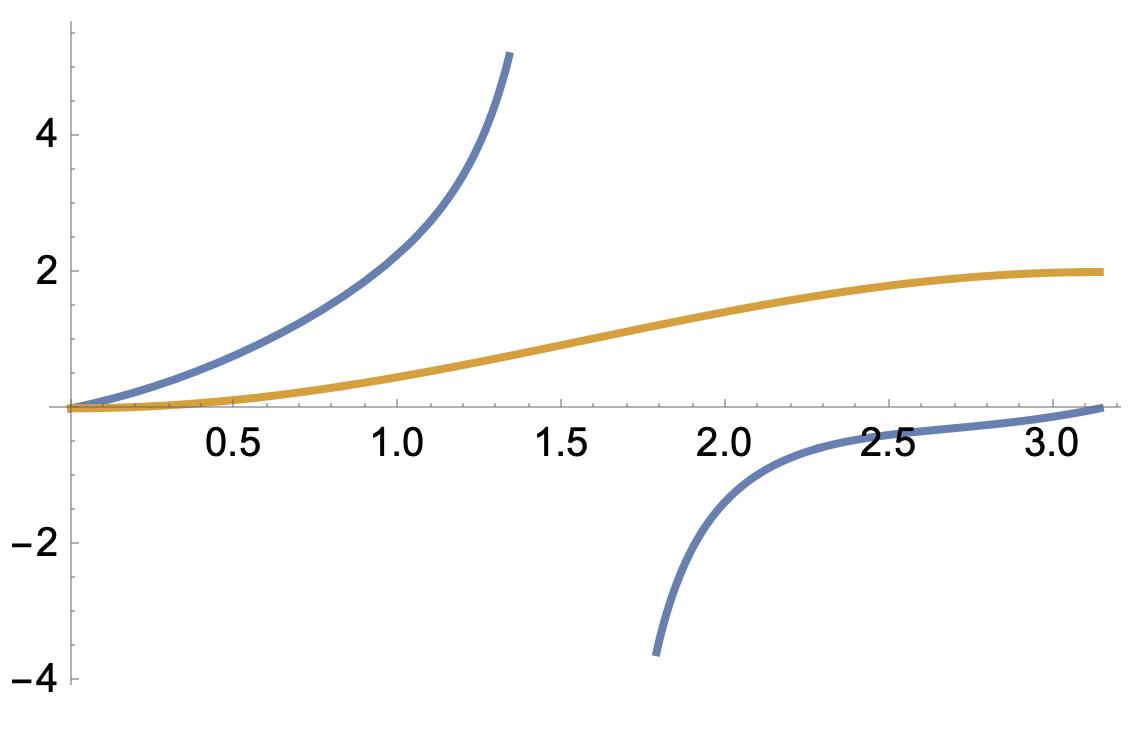
Kan sin^2x + Tan x förenklas till 1-cosx? Motivera.
Jag vet inte... Y värdet i en enhetscirkel i kvadrat+ höjden på y kateten för tangenten, kan det vara lika med 1- x värdet för samma triangel. Känns konstigt men.
Jämför värdena de båda uttrycken kan anta
Jo, det kan man ju göra
Fast jag måste motivera det på något sätt
Vad har du kommit fram till?
x=pi/2 ger svaret på frågan;
Om man tar något godtyckligt. 45°.
Så räknar man bara och kollar, då kommer man fram till att: sin^2(45°) + tan(45°) = 0.5+1 = 1.5
Sedan då 1 - cos(45°) = 0.293.
Går det att förenkla så hade det gått för alla vinklar. Så svaret är att det går inte. Motiveringen är.. att definitionen av funktionerna medför att det inte går.
Det stämmer att det inte går. Jag tycker att en bra motivering kan vara följande:
För vinkeln x = 45° så gäller det att uttrycket sin2(x)+tan(x) har värdet 1,5 och uttrycket 1-cos(x) har det ungefärliga värdet 0,29.
Dessa värden är inte lika, vilket innebär att uttrycken inte är identiska, vilket i sin tur betyder att det ena inte kan skrivas om till det andra.
Okej, jag visste inte att det var tillåtet att göra på det här sättet. Genom att pröva sig fram, så att säga.
Tack.
Det är helt OK att visa att något inte gäller med hjälp av motexempel, som i det här fallet.
Däremot går det inte att visa att något gäller enbart med hjälp av exempel.
Aha okej :)



