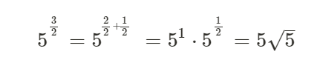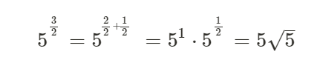Kan någon förklara detta för mig (potenser med rationella tal)
Hej,
Jag försöker förstå nedan avsnitt:

Jag hänger med på detta:
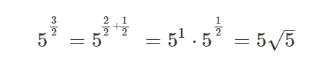
Men inte detta:

Hade nån kunnat utveckla ovan för mig? tack!
LumpyFishSwimming skrev:Hej,
Jag försöker förstå nedan avsnitt:
Jag hänger med på detta:
Men inte detta:
Hade nån kunnat utveckla ovan för mig? tack!
Är du med på att (x2)3 = x2*x2*x2 = x6 =x2*3?
Smaragdalena skrev:LumpyFishSwimming skrev:Hej,
Jag försöker förstå nedan avsnitt:
Jag hänger med på detta:
Men inte detta:
Hade nån kunnat utveckla ovan för mig? tack!
Är du med på att (x2)3 = x2*x2*x2 = x6 =x2*3?
det är jag, men jag hänger inte riktigt med på hur 3:an hamnar i exponenten. Jag gissar att det är för att man har faktoriserat bråket, och därmed kan lägga 3:an som exponent?
det är jag, men jag hänger inte riktigt med på hur 3:an hamnar i exponenten. Jag gissar att det är för att man har faktoriserat bråket, och därmed kan lägga 3:an som exponent?
Vad menar du? Trean ÄR exponenten i mitt exempel.
Smaragdalena skrev:det är jag, men jag hänger inte riktigt med på hur 3:an hamnar i exponenten. Jag gissar att det är för att man har faktoriserat bråket, och därmed kan lägga 3:an som exponent?
Vad menar du? Trean ÄR exponenten i mitt exempel.
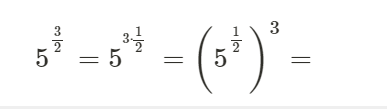
menar här.
Det är en logritmlag potenslag, som du behöver lära dig både fram- coh baklänges. Den finns på ditt formelblad, men du behöver känna igen när den är användbar, som t ex nu.
Smaragdalena skrev:Det är en logritmlag, som du behöver lära dig både fram- coh baklänges. Den finns på ditt formelblad, men du behöver känna igen när den är användbar, som t ex nu.
men logaritmer används väl när en variabel utgör exponenten?
Du har rätt, jag borde ha skrivit potenslag. Potenslagar och logaritmlagar är så nära släkt att jag gjorde fel. Jag fixar i mitt förra inlägg!
Smaragdalena skrev:Du har rätt, jag borde ha skrivit potenslag. Potenslagar och logaritmlagar är så nära släkt att jag gjorde fel. Jag fixar i mitt förra inlägg!
Tack, du menar att jag ska använda denna baklänges?
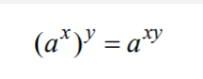
Välj x = 3 och y = ½ så kan du använda den lagen baklänges för att gå från 53*½ till (5½)3 (fast man har ändrat på ordningen , men det spelar ingen roll).