Kan man inte räkna ut riktning på t.ex. magnetfält?

naytte skrev:

Vad är det för matematik/ekvationer jag behöver då? 

Jag inser att matematiken antagligen är väldigt avancerad men jag skulle gärna vilja veta ändå och åtminstone försöka mig på den.  

Högerhandregeln kan formuleras med kryssprodukt, till exempel Lorentzkraften på en partikel med laddning q och hastigheten v är ${\vec F}_{\rm \!Lor} = q {\vec v} \times {\vec B},$ det är inte så avancerat.

Matematiken för Maxwellekvationer är vektoranalys.

Okej, tack så mycket! Jag ska läsa på om Maxwells ekvationer m.m.

En fråga bara om just Lorenzkraften, eftersom du tog upp det som exempel. När man räknar på laddningen, räknar man då på beloppet av laddningen eller ska man ha med tecken också? För när vi räknade på t.ex. Coulombs lag i Fysik 1 blev vi tillsagda att inte räkna med tecken på laddningen. Men här verkar det göra lite större skillnad än vid Coulombs lag...

naytte skrev:
För när vi räknade på t.ex. Coulombs lag i Fysik 1 blev vi tillsagda att inte räkna med tecken på laddningen.  

Det låter konstigt. Det finns många frågor här på Pluggakuten i Fysik 1 där man ska räkna med laddningens tecken.

Jaha, ja då verkar det verkligen konstigt.

Men jag tolkar ditt svar då i alla fall som att man ska räkna med laddningens tecken?

Man kan göra så att man räknar ut kraftens storlek utan att bry sig om tecken och till sist funderar ut riktningen genom att bara betrakta partiklarnas laddningar - lika eller olika.

Annars sitter man där med t.ex. "a påverkar b med kraften -5 N", "vad betyder det nu igen" och risken för fel är en aning större då.

Det kanske är det som ligger bakom dylika råd från lärarna.

Mycket möjligt. Men just i det här fallet har det väl en ganska stor påverkan om skalären $q$ är positiv eller negativ? Eftersom vi utökar det hela till mer än två dimensioner.

För att vara tydlig: jag tror att du måste ha missuppfattat din lärare.

naytte skrev:

Vad är det för matematik/ekvationer jag behöver då? 

Det är egentligen typ bara matriser som man räknar på för att ta reda på riktningar.

naytte skrev:

... blir ganska irriterad av de här handreglerna, t.ex. högerhandsregeln, eftersom jag tycker de är ologiska och godtyckliga. 

De är hjälpredor som utformats och populariserats av en ingenjör för att göra arbetet enklare. De är varken ologiska eller godtyckliga men kanske har förklarats på ett dåligt sätt. I många böcker så ska man envisas med att separera dem som tre eller fler olika när de alla bygger på samma bakomliggande matematik egentligen.

Det är som Pieter skrev kryssprodukten mellan vektorer som lägger grunden för det. Om en vektor längs med $x-axeln$ kryssas med en vektor längs med $y-axeln$ är resultatet en vektor längs med $z-axeln$. Detta kallas också för ett högerhandssystem.

Om en partikel med laddning $q$ rör sig med en konstant hastighet $v$ i ett magnetfält med fältstyrka $B$ utsätts den för en kraft med storlek:

$F=qvB$

Du kan också uttrycka det som en kryssprodukt:

$\vec{F}=q\vec{v}\times \vec{B}$

Kraftvektorn som bildas av kryssprodukten kommer alltid vara vinkelrät till både hastighet och magnetfält. Ta denna bild till exempel:

Fråga: Är partikeln positivt eller negativt laddad?

Med högerhandsregeln har du svaret nästan direkt. Med matematiska operationer kan du räkna dig fram till det. I detta fall är båda ganska enkla.

SaintVenant skrev:

naytte skrev:

... blir ganska irriterad av de här handreglerna, t.ex. högerhandsregeln, eftersom jag tycker de är ologiska och godtyckliga. 

De är hjälpredor som utformats och populariserats av en ingenjör för att göra arbetet enklare.  

Du syftar nog på Fleming: https://en.wikipedia.org/wiki/John_Ambrose_Fleming 

Men något sådant måste ha funnits tidigare. Jag gissar att redan Faraday hade något för att beskriva magnetiska fenomen. Eller så struntade han i det.

Det är inte klokt tycker jag att skolan ägnar så mycket möda åt detta. Vanligtvis var det enda som jag behövde veta att kraften är åt andra hållet om man ändrar strömriktningen osv.

Tack så hemskt mycket för era svar, @SaintVenant och @Pieter Kuiper!

Angående din fråga, @SaintVenant:

Jag är inte riktigt säker på om jag har räknat rätt, för jag har inte räknat så mycket på matriser tidigare, men jag skulle säga att laddningen är negativ med följande resonemang:

Eftersom kraften är vinkelrät mot både magnetfältets riktning och mot hastigheten måste den se ut på följande vis:

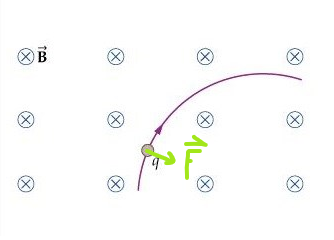
Då har kraften en positiv x-komponent och en negativ y-komponent, så vi kan skriva den som:

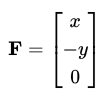
På samma sätt kan vi se att hastighetsvektorn bara har positiva komponenter och att magnetfältsriktningen har en negativ z-komponent. Då kan vi ställa upp det som:

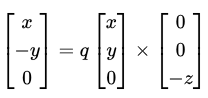
Beräknar man kryssprodukten får man (jag) följande vektor som resultat:

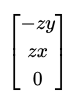
Eftersom tecknen på kraftvektorns komponenter är motsatta måste laddningen på q vara negativ.

Tillägg: 7 nov 2023 09:14

Oj, den tyckte verkligen inte om den latexkoden. Ska skriva om.
EDIT: Fixat.

Det är bättre att skriva ${\vec B} = \begin{bmatrix} 0 \\ 0 \\ -B \end{bmatrix}, \ {\vec v} = \begin{bmatrix} v/\sqrt{2} \\ v/\sqrt{2} \\ 0 \end{bmatrix},$osv.

Förstår, det blir kanske förvirrande att använda samma variabler för alla. Men varifrån får du att hastighetens komponenter blir $\displaystyle v/\sqrt2$?

naytte skrev:

 varifrån får du att hastighetens komponenter blir $\displaystyle v/\sqrt2$?

Det var de ungefär i ritningen. Du kan förstås ta vad du vill, t ex ${\vec v} = \begin{bmatrix} v_{\rm x} \\ v_{\rm y} \\ 0 \end{bmatrix} = \begin{bmatrix} v \\ 2v \\ 0 \end{bmatrix}.$

Okej, förstår! Men stämde mitt resonamng ändå med laddningen?

Eller nej det borde vara en positiv laddning.

Hastigheten $\vec{v}$ är riktad snett uppåt höger $\nearrow$.

$\vec{v}=(v_x,v_y,0)$

Magnetfältet är riktat rakt in i pappret (vi markerar med ett minustecken och låter $B_z>0$ så här

$\vec{B}=(0,0,-B_z)$

Kraften är riktad snett nedåt åt häger $\searrow$.

$\vec{F}=(F_x,-F_y,0)$

Kryssprodukten blir $\vec{F}=(F_x,-F_y,0)=q\vec{v}\times\vec{B}=(-qv_yB_z,qv_xB_z,0)$.

Vilket tecken måste $q$ ha? I vårt system är $v_z,v_y,B_z$ större än noll enligt bild.

Ja, det var så jag gjorde först också men borde inte magnetfältets koordinat vara positiv? Alltså:

$\stackrel{\rightharpoonup }{B}=(0, 0, B_z)$

Det beror på om du vill låta $B_z$ i sig innehålla teckeninformationen. Men det är två saker som är viktigt att hålla ordning på, riktningen på- och uppräkningsordningen av koordinataxlarna.

Ett högerorienterat system ser ut så här (notera i vilken ordning x,y och z ligger och hur de pekar)

xy-planet är papprets plan och magnetfältet är riktat nedåt utmed z-axeln. I negativ riktning.

D4NIEL skrev:

 xy-planet är papprets plan  

Det ser annorlunda ut när jag visualiserar det. I mitt huvud hamnar z-axeln i papprets plan.

naytte skrev:

Ja, det var så jag gjorde först också men borde inte magnetfältets koordinat vara positiv? Alltså:

$\stackrel{\rightharpoonup }{B}=(0, 0, B_z)$

Magnetfältet i figuren pekar nedåt, dvs i negativ $\hat{z}$led. 

Man får ju naturligtvis vända och vrida på sitt koordinatsystem, men det naturliga för de flesta är att välja x åt höger och y uppåt pappret, varvid z-axeln pekar upp mot betraktaren, vinkelrätt mot pappret. I den här bilden pekar z-axeln mot betraktaren. Magnetfältet (kryssmarkerat) pekar därmed i negativ $\hat{z}$-led.

Eftersom tecknen på kraftvektorns komponenter är motsatta måste laddningen på q vara negativ

Du märker kanske nu varför att räkna sig fram till det fort kan bli mycket krångligare än att bara använda en kom-ihåg-regel. Det är inte att tecknen är motsatta som avslöjar partikelns laddning, det är riktningen på kraften. Tecknen hade i detta fall varit motsatta oberoende om partikelns laddning var positiv eller negativ.

Använd högerhanden och sätt tummen i hastighetens riktning, pekfinger i magnetfältets riktning och långfingret i kraftens riktning. Du får då ut kraften upp till vänster och därför kan omöjligt partikeln vara positiv. Den måste vara negativ.

Tips: För en negativ partikel kan man använda vänsterhanden istället. Då gör du du samma sak (tumme, pekfinger, långfinger) och får kraftens riktning som ned till höger.