Kan man faktorisera detta uttryck? :) 2
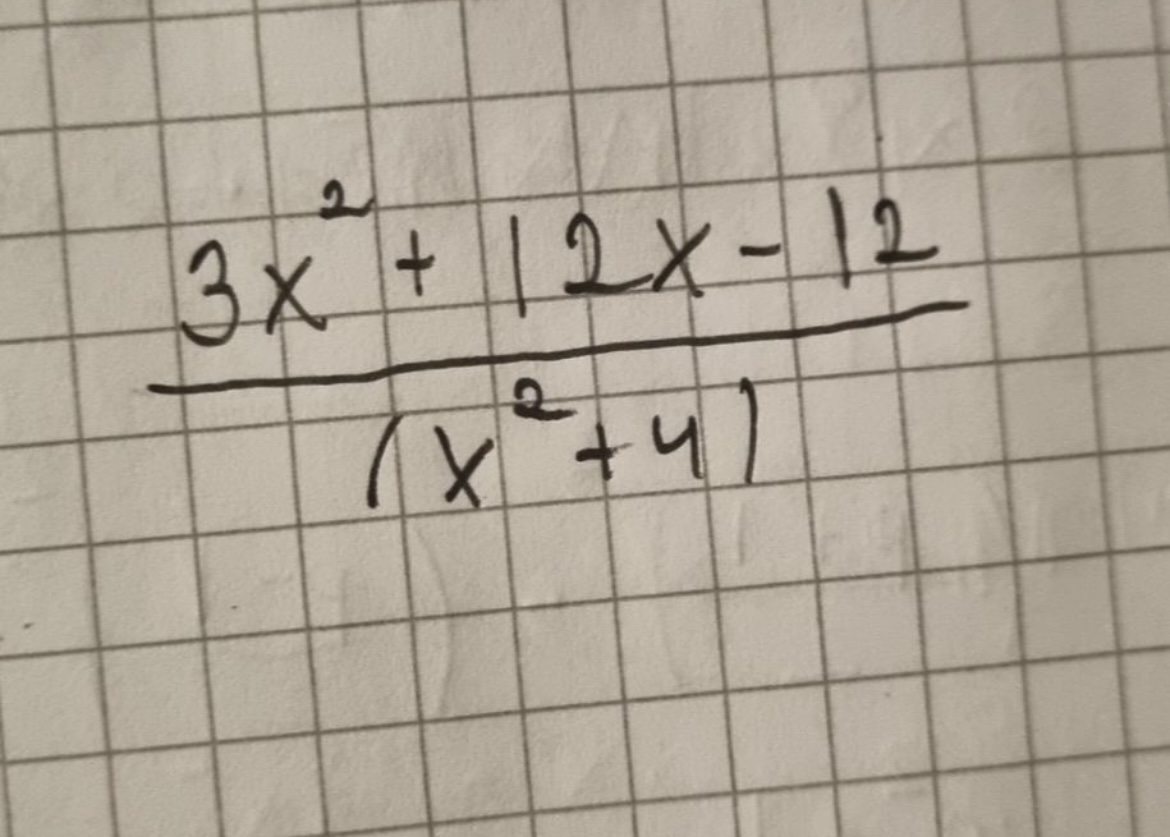
Är någon siffra otydlig är det vara att fråga!
Man kan hitta nollställena till täljaren och på så vis faktorisera den, men man kommer inte längre än så.
Jag tror jag kan läsa dina siffror. Kan du ta en bild på uppgiften i boken i alla fall?
Har tyvärr gömt boken så har bara uppgiften! Men tack så mycket för hjälpen, hur blir det om man hittar nollställena till täljaren?😊
Man kan bryta ut 3: 3(x2+4x-4).
Kan du använda pq-formeln på x2+4x-4?
Jag har tidigare aldrig använt pq-formeln men hur blir det om man använder den?😊
Pq-formeln: Andragradsekvationen har lösningarna .
Du vill hitta nollställena till uttrycket , dvs du vill lösa ekvationen .
Här är tydligen och .
Pq-formeln ger då att
Kommer du vidare därifrån?
Linnea0025, försök ge dina trådar unika namn så gott det går. Om det inte är möjligt kan du numrera de som jag gjort ovan. /moderator
Yngve skrev:Pq-formeln: Andragradsekvationen har lösningarna .
Du vill hitta nollställena till uttrycket , dvs du vill lösa ekvationen .
Här är tydligen och .
Pq-formeln ger då att
Kommer du vidare därifrån?
Ja! Tack så mycket!
Citatfel korrigerat. /Dracaena




