Kan f(x) verkligen göras kontinuerlig i x=0?

Halloj igen!

Sitter med denna uppgift:

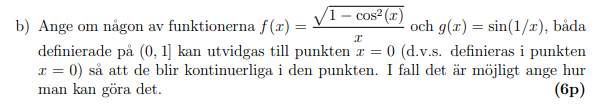
$g(x)$ kan ju trivialt inte göras kontinuerlig, så jag fokuserar på $f(x)$. När jag tittar på höger- och vänstergränsvärdena tänker jag:

$\displaystyle \lim_{x \to 0^-} \frac{\sqrt{\sin^2x}}{x}=\lim_{x \to 0} \frac{-\sin x}{x}=-1$

Och för högergränsvärdet:

$\displaystyle \lim_{x \to 0^+} \frac{\sqrt{\sin^2x}}{x}=\lim_{x \to 0} \frac{\sin x}{x}=1$

Min slutsats är att eftersom höger- och vänstergränsvärdet inte överensstämmer så kan funktionen inte göras kontinuerlig i $x=0$. I facit har de dock skrivit att båda gränsvärdena går mot $1$, och att funktionen således kan göras kontinuerlig. Men det kan väl inte stämma? Har de bara gjort ett elementärt misstag eller har jag gjort fel?