Jordens ålder baserat på halveringstid av Uran (Exponentiell funktion)
Hej!
Har en uppgift som lyder "För uran-238 är halveringstiden 4,5x109 år och för uran-238 är den 0.7x109 år. För närvarande innehåller jordens uran-malmer ungefär 140 gånger så många atomer av uran-238 som av uran-235. Uppskatta med hjälp av denna data jordens ålder om man antar att det vid jordens uppkomst bildades lika många atomer av vardera slag."
Eftersom mängden uran-238 idag, är 140 gånger större än mängden uran-235 så gäller följande:
Behöver ju ställa upp två exponentiella funktioner (Y=Cat) för att få två värden som jag kan dividera varandra med. För at få ut vad "t" är. Alltså hur många år halveringen pågått vilket inom uppgiftens ramar = jordens ålder.
Om mängden från start = A, gäller
Hur kommer jag fram till vad "t" blir för vardera sort? Att endast stoppa in halveringstiden ger inte rätt svar enligt facit.
Oftast används denna formel för att uppskatta mängden partiklar som finns efter tiden t:
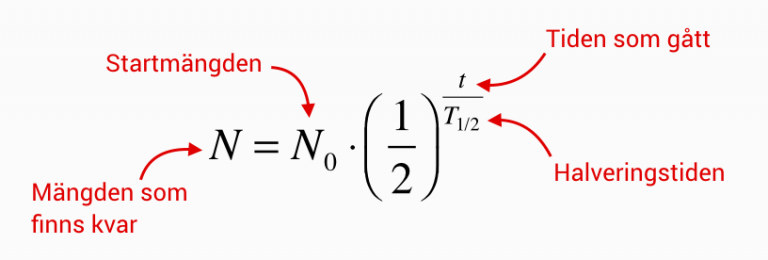
Hjälper det dig att komma vidare?
fner skrev:Oftast används denna formel för att uppskatta mängden partiklar som finns efter tiden t:
Hjälper det dig att komma vidare?
Ja, tack!


