Jämnvikt - Kraftmoment
En person ställer upp ett bord med en tung planka på. Sedan ställer han sig längst ut på plankan. Personen väger 76kg, plankan är 3,6m lång och väger 22kg.
"Hur långt kan personen maximalt skjuta ut plankan utan att den tippar när han ställer sig längst ut på den?"
MA=F*l
F=mg
m1=22kg
m2=76kg
m1gl1 =m2gl2. (Dela med g)
m1l1=m2l2
Jag letar efter ett uttryck på l och får det till: (väljer att uttrycka längderna i form av "x"). Lite osäker om detta blir rätt, vilket jag antar att det är eftersom svaret blir fel.
m1x=m2(3,6-x)?
m1x=3,6m2-m2x
m1x+m2x=3,6m2
x(m1+m2)=3,6m2
x=(3,6*76)/(22+76)=2,79m
Så sidan som personen står på blir alltså 3,6-2,79=0,81m=81cm.
Svaret ska bli 40,4cm. Vad är det jag gör fel? (Just nu är min enda gissning att uttrycket för längden blir fel, men jag vet inte varför)
Mvh
Skepnad skrev:
Så sidan som personen står på blir alltså 3,6-2,79=0,81m=81cm.Svaret ska bli 40,4cm. Vad är det jag gör fel?
Kanske att du inte ritade.
Pieter Kuiper skrev:Skepnad skrev:
Så sidan som personen står på blir alltså 3,6-2,79=0,81m=81cm.Svaret ska bli 40,4cm. Vad är det jag gör fel?
Kanske att du inte ritade.
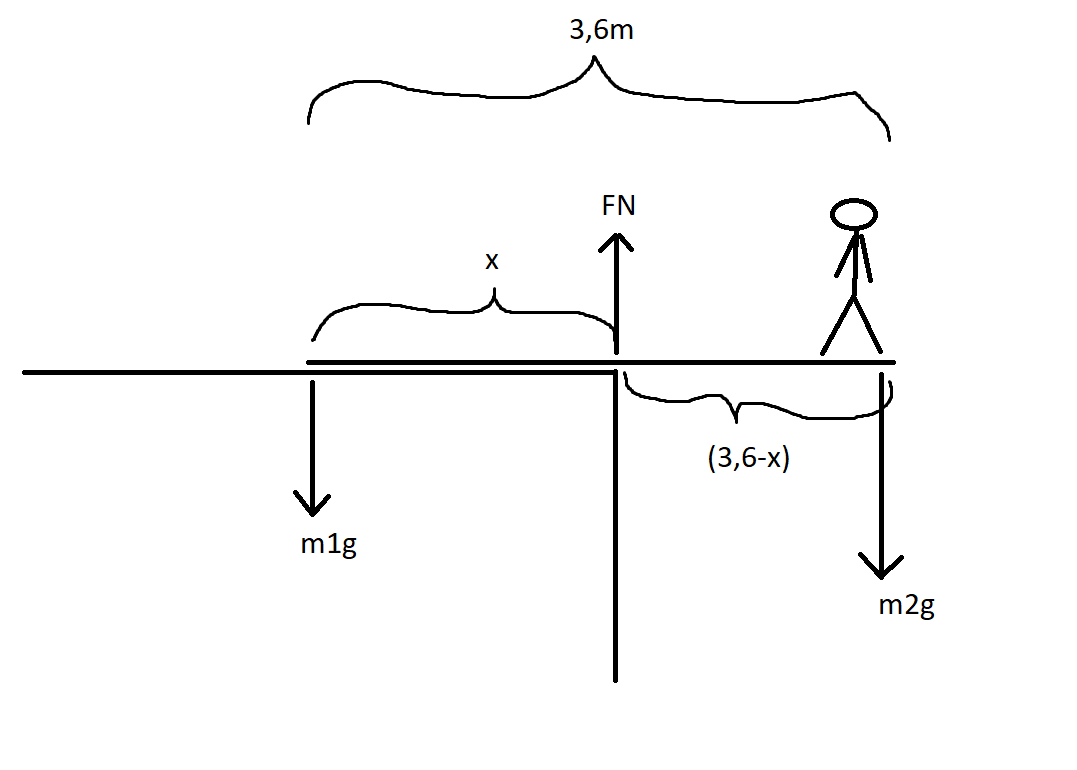Jag blir inte så mycket klokare tyvärr. Efter att jag räknat ut x så ska ju längden som personen står på fortfarande vara 3,6-x. Och byter jag plats på uttrycken för längden så får jag fortfarande samma svar.
Tankevurpa
Men slutsatsen av tankevurpan blir att 3,6-x inte borde vara uttrycket för längden där personen står.
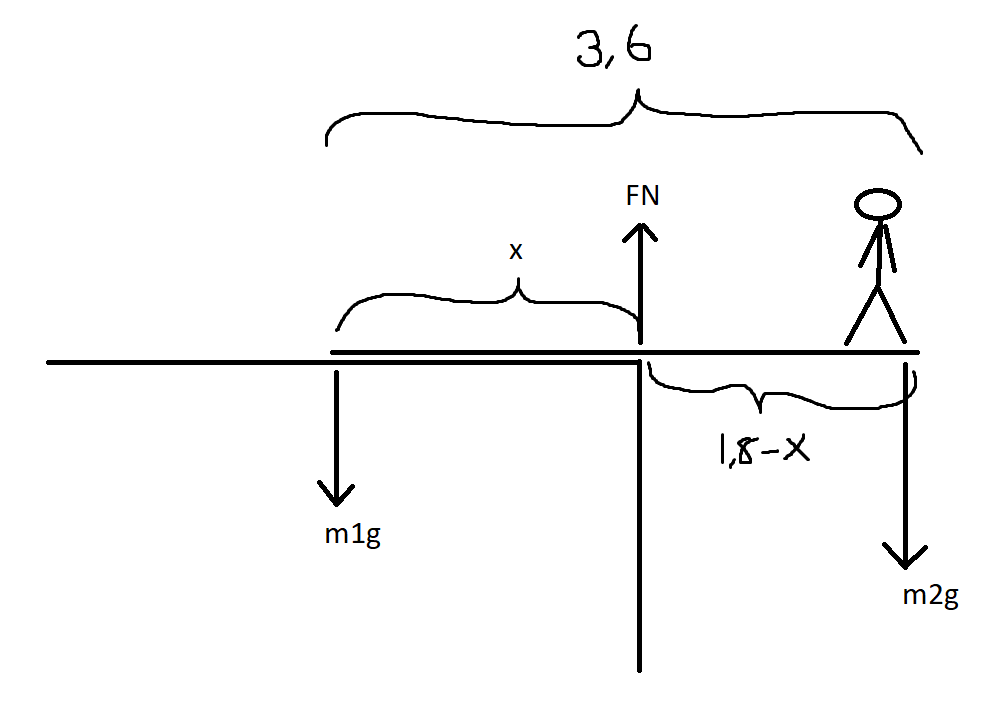Med (1,8-x) får jag rätt svar. (Därför jag alltid var 1/2 faktor från svaret). Men hur funkar det om x>1,8? Då blir högra sidan negativ?
Edit: Allt blir bara grötigt i huvudet just nu. Tror det är dags för en promenad så får jag titta på det senare och se om det blir klarare. (Bollar bara med siffor just nu istället för att se "helhetsbilden")
Efter en promenad och lite mat så löste det sig och jag förstår varför det går ihop... Hjärnan blir visst inte så kry efter att ha pluggat en dag utan paus.
Bra!
Så man ska räkna med att plankans tyngd har sitt angreppspunkt vid tyndpunkten (alltså i mitten).
