Jag vet inte vart jag gör/tänker fel på denna uppgift ?

Du skriver att CD = 3,6 cm och att DP =:5,2 cm.

Det kan inte stämma.

Ett annat fel är att du beräknar x, men x är ju lika med AP. Du ska istället bestämma AB.

Ladda upp en bild på uppgiften och visa även den bild fu själv har ritat.

Ett

==== Fortsättningen ====

Det stämmer att kordadatsen lyder AP*BP = CP*DP, men du använder den fel.

Du vet att

• BP = 4,4 cm
• CD = 3,6 cm
• DP = 5,2 cm

I din bild ser du att CD = CP+DP, vilket betyder att CP = CD-DP.

Kordasatsen blir då

AP*BP = (CD-DP)*DP

Du kan nu beräkna AP och ta dig vidare därifrån.

Hej, tack för svaret. 

här kommer en bild på uppgiften

och här kommer en bild på min bild:

****
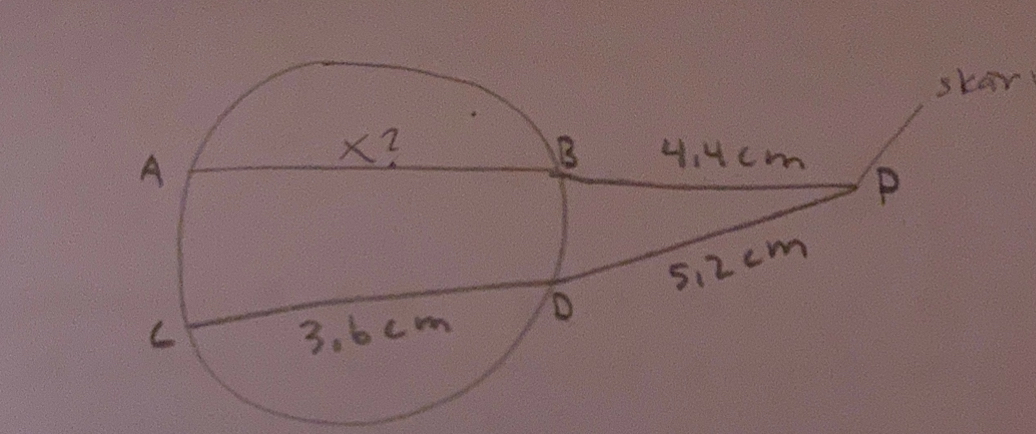jag tänker att eftersom att detta gäller:
AP * BP = CP * DP  alltså:
A till P & värden där som då är x & 4,4 
B till P & värden där som då är 4,4 
C till P & värden där som då är 3,6 & 5,5 
D till P & värden där som då är 5,2 

 så typ : x*4,4 (4,4) =3,6*5,2(5,2) ?


___________

Hur menar du att de blir - ? alltså:
I din bild ser du att CD = CP+DP, vilket betyder att CP = CD-DP.

Aha, jag trodde att kordorna skulle skära varandra inuti cirkeln.

Men nu förstår jag 

Att skärningspunkten ligger utanför cirkeln ger oss istället att

• $AB = AP-BP$
• $CP=CD+DP$

Med "ytterkordasatsen" har vi att

$AP\cdot BP = CP\cdot DP$

Om vi nu löser ut den okända storheten $AP$ så får vi $AP=\frac{CP\cdot DP}{BP}$

Slutligen får vi $AB=AP-BP=\frac{CP\cdot DP}{BP}- BP$.

Kommer du vidare själv därifrån?

Så.. för att jag ska få fram AB så tar jag:

AP-BP =CD+DP och räknar ut den ekvationen? så borde jag få fram AB? alltså:

(X*4,4) - 4,4 = (3,6*5,2) + 5,2 

Förstår inte det sista alltså de här: 

AP = CP*DP / BP 

sen

AB= AP -BP = CP*DP/BP -BP 

förstår inte varför jag ska ta delat ?och hur liksom ska man veta att man ska göra så?

EDIT - Det står fel i steg 1, 5 och 7 nedan. Jag låter det stå kvar eftersom det är kommenterat i senare svar.

============

Tankegången kan vara att du vill ta fram ett uttryck för $AB$.

I bilden ser du att $AB=AP-BP$.

Du känner till $BP$ men inte $AP$.

Du kan få fram ett uttryck för $AP$ med hjälp av beräkningsstegen nedan.

Är det då något/några av följande steg som du fastnar på?

1. Från bilden ser vi att $AB+BP=AP$, vilket ger oss att $AB=AP-DP$
2. Från bilden ser vi att $CD+DP=CP$
3. Kordasatsen lyder $AP\cdot BP=CP\cdot DP$
4. Om vi dividerar båda sidor i kordadatsen med $BP$ så får vi $AP=\frac{CP\cdot DP}{BP}$
5. Om vi nu sätter in detta i uttrycket för $AB$ från steg 1 så får vi $AB=\frac{CP\cdot DP}{BP}-DP$
6. Vi vet att $CP=CD+DP=3,6+5,2=8,8$, att $DP=5,2$ och att $BP=4,4$
7. Om vi nu sätter in dessa värden i uttrycket från steg 5 så får vi $AB=\frac{8,8\cdot5,2}{4,4}-5,2=6,0$

Tack för stegen, blir enklare att se. 

På steg 1)  AB+BP = AP och det förstår jag, men sen står det AB=AP-DP, det blir väl AB= AP-BP och inte DP? för jag antar att AB och BP är lika långa? varför står det -DP? den är ju på andra sidan?

Naturens skrev:

På steg 1)  AB+BP = AP och det förstår jag, men sen står det AB=AP-DP, det blir väl AB= AP-BP och inte DP?

Du har rätt, jag sjrev fel. Och då är även uttrycket i steg 5 samt värdena i steg 7 fel.

för jag antar att AB och BP är lika långa?

Nej, de behöver inte vara lika långa.

varför står det -DP? den är ju på andra sidan?

Se ovan.

så man går från steg:  AP *BP = CP * DP 
till                                   : AP = CP*DP / BP 

och nu, i steg 5) när man nu ska sätta in AB i uttrycket så står det: AB = CP*DP/BP - BP 
men i V.L stod det ju AP men antar att AP nu blir AB då BP är borta så förstår att den "byts ut" från AP till AB
men varför läggs -BP till ? och ska de då inte vara en -BP i V.L med?

Naturens skrev:

så man går från steg:  AP *BP = CP * DP 
till                                   : AP = CP*DP / BP 

Ja, det stämmer

och nu, i steg 5) när man nu ska sätta in AB i uttrycket så står det: AB = CP*DP/BP - BP 
men i V.L stod det ju AP men antar att AP nu blir AB då BP är borta så förstår att den "byts ut" från AP till AB
men varför läggs -BP till ? och ska de då inte vara en -BP i V.L med?

Nej, tvärtom.

Du har från (det korrigerade) steg 1 att $AB=AP-BP$

Du har i steg 4 tagit fram ett uttryck för $AP$, nämligen $AP=\frac{CP\cdot DP}{BP}$

I steg 5 ersätter vi $AP$ i steg 1 med $\frac{CP\cdot DP}{BP}$ från steg 4.

======

Ett enklare exempel som illustrerar samma sak:

Om vi har att x = 2 och vi vill ta fram värdet av uttrycket x+6 så kan vi ersätta x med 2 i uttrycket och vi får då 2+6 = 8

okej, så uttrycket blir då 
CP * DP / BP och den ekvationen blir vad AB är ?

Alltså svaret som ekvationen CP*DP/BP ger, är alltså vad AB är?

Naturens skrev:

okej, så uttrycket blir då 
CP * DP / BP och den ekvationen blir vad AB är ?

Nej, CP*DP/BP är ingen ekvation, det är ett uttryck.

Och som vi har sett i steg 4 så är detta uttryck lika med AP.

Alltså svaret som ekvationen CP*DP/BP ger, är alltså vad AB är?

Nej, eftersom AB = AP - BP (steg 1) och AP = CP*DP/BP (steg 4) så är AB = CP*DP/BP - BP.

Säg till om du behöver mer hjälp med att räta ut kvarvarande frågetecken.

Jag fick sammanfatta det lite med mina egna ord för att liksom förstå tänket bättre, för ditt sätt att tänka, ger rätt svar och mitt sätt ger fel svar.

Och jag tänker att:

På samma sätt som CP är :  CP= CD+DP 
så är även                   AP      :  AP= AB+BP 

Jag vet vad CP är då sidan CD =3,6 och DP = 5,2 
Jag vet inte vad AP är då sidan AB= x eller ? och BP är 4,4 (det är inte komplett) 

Så för att få reda på vad APs AB sida är, behöver jag "ett uttryck som är en annan variant av kordasatsen".
Detta då kordasatsen säger: AP*BP=CP*DP. Men om jag skapar en ekvation och sätter in de värden jag har från figuren in till AP*BP=CP*DP, så blir det fel, och det var här jag tänkte fel. Jag tänkte att jag bara kunde sätta in värden från figuren och lösa ut x, då jag ger AB sidan ett värde X. Genom att sen lösa ekvationen skulle jag få fram vad X (AB sidan) är. Men det tänket är fel, vet inte varför, men det funkar inte i denna uppgift. Jag tänkte liksom: Okej Kordasatsen är: AP*BP=CP*DP     så gör bara så här         x*4,4 (4,4)=3,6*5,2(5,2)        = FEL!

"En annan variant av kordasatsen" är vad jag kallar det du visa. 
Om kordasatsen är AP*BP=CP*DP och jag vet att AP är både AB+BP.
Så vill jag först få AP själv i V.L till ett uttryck som då blir: AP=CP*DP/BP
Sen vill jag få bort värdet av BP i från AP för att få AB själv i AP och då måste jag lägga in -BP i uttrycket på slutet dvs: 

AP=CP*DP/BP -BP

Sen sätter jag värden på  CP*DP/BP -BP
och räknar fram vad AP blir -BP sidan, dvs AP blir vad AB är. När man räknat klart.
 
När jag tänkte så, vart de mindre rörigt i mitt huvud. 

TACK!!!!