Jag stöter på problem när jag konstruerar lösningar till dereverings uppgifter, hur ska jag göra?
Jag får många gångar ekvationer som dessa, som jag ska derivera och kolla extrem punkter på.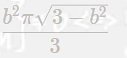
Där jag måste använda mig av kedje-regeln. Det slutar med att jag använder grafiska verktyg för att lösa dem tillslut, då kedjeregeln är utanför min kurs. Här är två exempel uppgifter det har slutat på det beskrivna sättet för mig.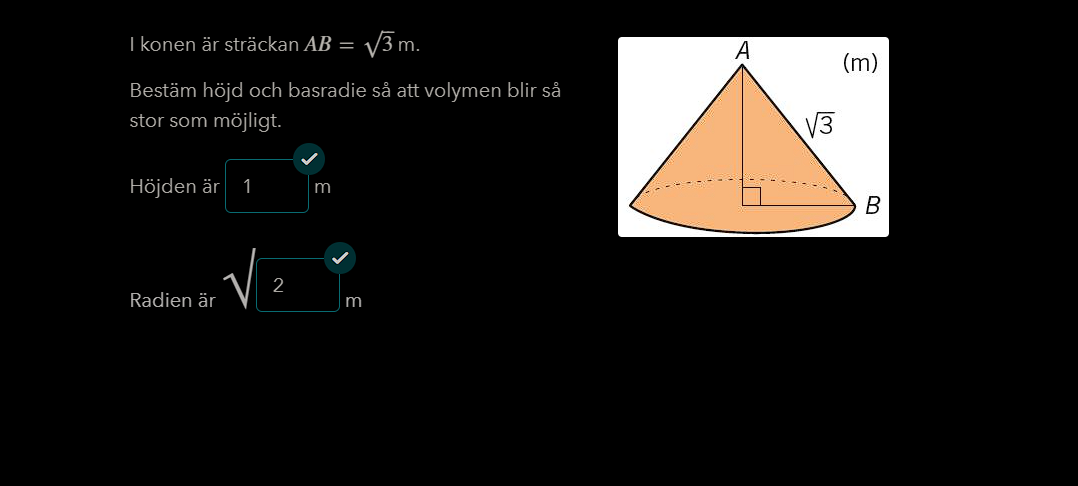
Jag känner att det borde vara enklare för mig att bara lära mig kedjeregeln, då det inte är så lätt att byta tankesätt inom matematiken. Skulle någon kunna då förklara hur man deriverar ekvationen på toppen, och sedan kanske beskriva problemet jag har och om det är vanligt.
Du ska inte behöva använda kedjeregeln i Matte 3.
Om konen:
Pröva att lösa ut höjden h istället för basradien r till att börja med.
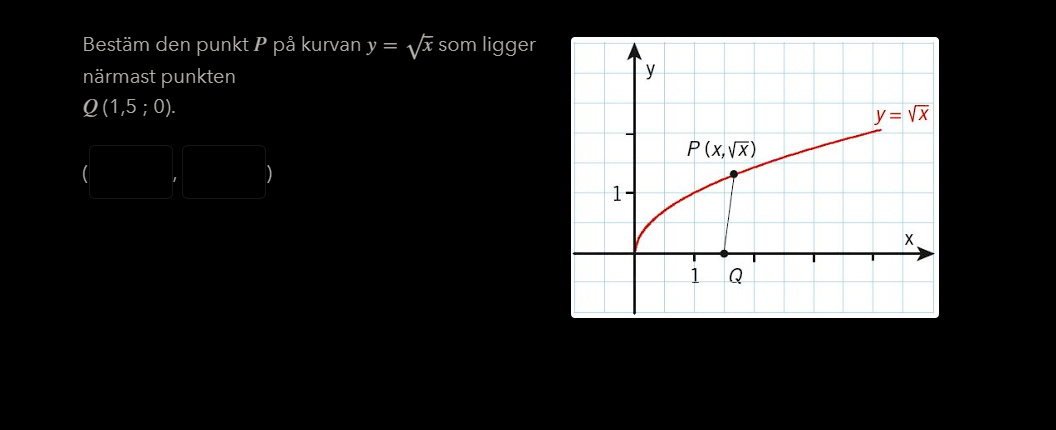
Gör en ny tråd för uppgiften om minsta avståndet om du vill ha hjälp med den.
Yngve skrev:Du ska inte behöva använda kedjeregeln i Matte 3.
Om konen:
Pröva att lösa ut höjden h istället för basradien r till att börja med.
Gör en ny tråd för uppgiften om minsta avståndet om du vill ha hjälp med den.
Min lösning fungerar, dock behöver kedje regel. Men hur kan jag förebygga att detta händer, så jag inte tänker ett långt tag sedan konstruerar så blir det omöjligt att lösa?
AlexanderJansson skrev:
Min lösning fungerar, dock behöver kedje regel.
Ja, men om du uttrycker volymen som funktion av höjden istället för radien så behöver du inte använda kedjeregeln. Pröva!
Men hur kan jag förebygga att detta händer, så jag inte tänker ett långt tag sedan konstruerar så blir det omöjligt att lösa?
Genom att lösa många uppgifter, så att du till slut känner igen mönstren.
