Jag har löst uppgifterna men har 1fråga
Hej,
Uppgiften är:
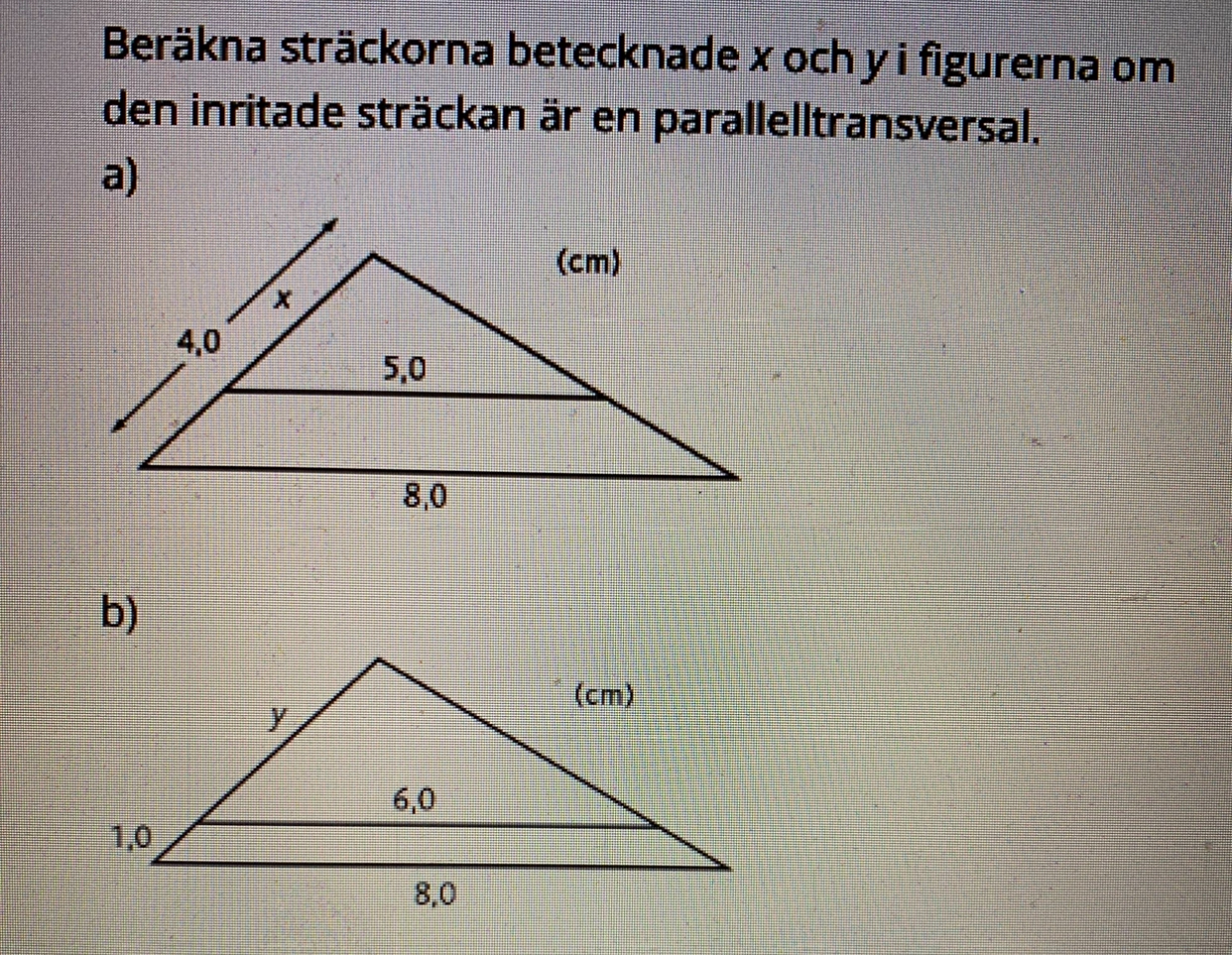jag har löst båda uppgifterna & fått rätt. Men jag har en fråga som jag hoppas jag kan få svar på.
jag löste uppgifterna med hjälp av transversalsatsen a/b=c/d
För att kunna ställa min fråga måste jag visa min ritning av triangeln (tar b uppgiften som ett exempel)
Jag rita upp triangeln & satte ut allt jag vet om den så här:
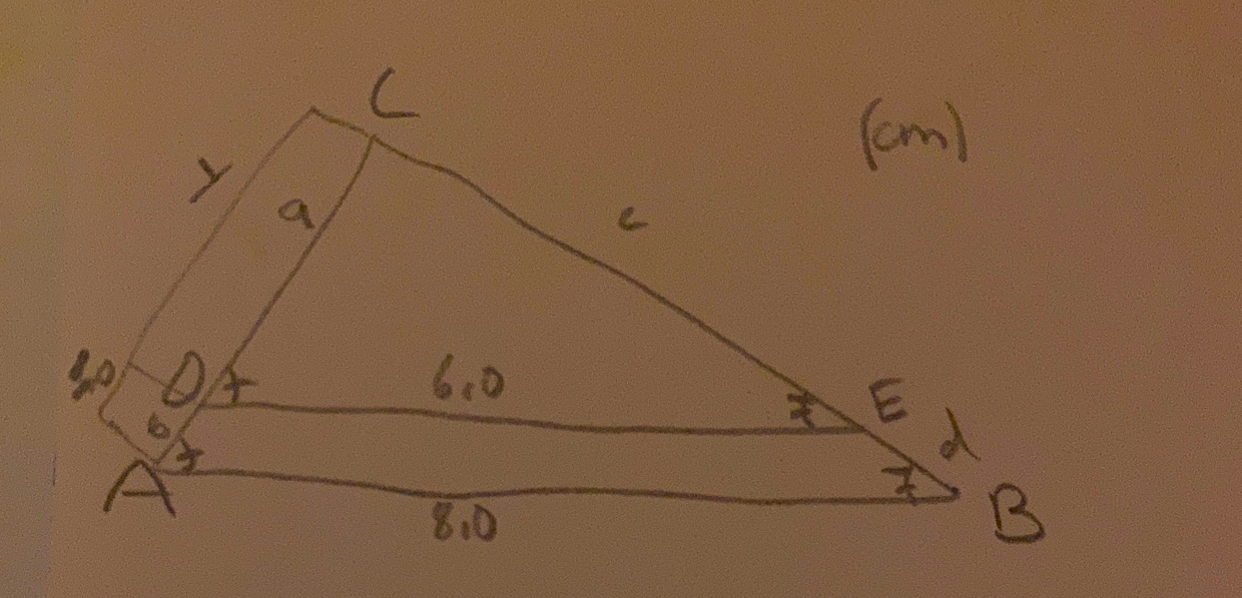
transversalsatsen : a/b=c/d är sträckorna/ sidorna på triangeln, så som jag ritat upp på bilden.
eftersom att jag inte har några mått på sida c,d blir det inga sidor jag kan använda mig av i en ekvation. Jag har dock värden på parallelltransversalen 6,0 och triangelns tredje sida 8,0 så jag använde de måtten.
ekvationen blev då:
y/1,0+y = 6,0/8,0
jag räkna ut det & fick fram rätt svar.
NU till min fråga. Transversalsatsen a/b=c/d gäller ju sidorna på triangeln som jag markerat med a,b,c,d och inte parallelltransversalen i triangeln & triangelns tredje sida. Hur kommer de sig att det funkar att lägga in dom värden i parallelltransversalen a/b=c/d NÄR sida 6,0 & sida 8,0 INTE är varken c sidan eller d sidan?
Hej.
Bra att du har löst uppgiften och jättebra att du frågar om metoden.
Du har korrekt använt ett likformighetssamband mellan sidlängder i de likformiga trianglarna ABC och DEC.
Transversalsatsen är ett specialfall av detta mer generella samband.
=====
Kommentar: Du måste använda parenteser runt nämnaren (1,0+y) om du skriver bråketvpå ovanstående sätt.
okej, men det gick att använda transversalsatsen på de 2 uppgifterna för att, jag har två likformiga trianglar?
Ja, om du har rvå likformiga trianglar så kan du alltid vända och vrida på den ena så att den hamnar "inuti" den andra.
Efter det så ser du vilka sträckor du i så fall ska använda i transversalsatsen och/eller topptriangelsatsen.
Men likformighetssambandet är mer generellt och därför viktigare att lära sig/träna på.
Vi kan säga så här:
Du kan klara dig utan att avända transversalsatsen/topptriangelsatsen men du kan inte klara dig utan att använda likformighetssamband.
Ur formelbladet Matte 2:
Jätte tack
