Jag är lite vilse med denna vinkel uppgiften.
 Uppgiften är: Bestäm vinkeln u
Uppgiften är: Bestäm vinkeln u
Jag är faktiskt helt vilse om vart jag ska börja här, det verkar vara 2 mindre trianglar och 1 stor fyrhörning, vart borde jag börja för att kunna komma igång?
Börja med den bredare, nedre triangeln. Två vinklar är givna i den, femton respektive sjuttioen grader. Hur stor är den tredje vinkeln? :)
Sen kan du ta den lilla längst till höger. Den ena vinkeln är 15 0 , en är 180 0 - 160 0 . Då får du fram den tredje trubbiga vinkeln. Sen tar du komplementvinkeln i triangeln intill.
Smutstvätt skrev:Börja med den bredare, nedre triangeln. Två vinklar är givna i den, femton respektive sjuttioen grader. Hur stor är den tredje vinkeln? :)
Så 15+71= 86
Den tredje blir 86 grader väl?
PeterG skrev:Sen kan du ta den lilla längst till höger. Den ena vinkeln är 15 0 , en är 180 0 - 160 0 . Då får du fram den tredje trubbiga vinkeln. Sen tar du komplementvinkeln i triangeln intill.
Så en är 15 grader,
180-160=20
Den tredje blir väl då
20+15= 35
180-35=145?
kärcherhaha skrev:Smutstvätt skrev:Börja med den bredare, nedre triangeln. Två vinklar är givna i den, femton respektive sjuttioen grader. Hur stor är den tredje vinkeln? :)
Så 15+71= 86
Den tredje blir 86 grader väl?
Inte riktigt. Det stämmer att summan av de två vinklarna är 86 grader, men vilken storlek måste då den tredje vinkeln ha?
Smutstvätt skrev:Börja med den bredare, nedre triangeln. Två vinklar är givna i den, femton respektive sjuttioen grader. Hur stor är den tredje vinkeln? :)
Men är det verkligen en triangel? Har den inte fyra hörn? Den som är 71 grader, den som är 160 grader och sedan den över 71 och den till höger av den som är 160
Smutstvätt skrev:kärcherhaha skrev:Smutstvätt skrev:Börja med den bredare, nedre triangeln. Två vinklar är givna i den, femton respektive sjuttioen grader. Hur stor är den tredje vinkeln? :)
Så 15+71= 86
Den tredje blir 86 grader väl?Inte riktigt. Det stämmer att summan av de två vinklarna är 86 grader, men vilken storlek måste då den tredje vinkeln ha?
180-86= 94
Isåfall?
Precis! Hur stor är då den vinkel som ligger precis ovanför denna vinkel? Hur stora är de andra vinklarna i den övre, lilla triangeln?
Smutstvätt skrev:Precis! Hur stor är då den vinkel som ligger precis ovanför denna vinkel? Hur stora är de andra vinklarna i den övre, lilla triangeln?
Den som ligger över den som är 71? Det är väl den som är 94?
Jag är osäker på jag ska räkna ut de andra vinklarna i den övre triangeln, är det inte något med att plusa ihop yttervinklar och sedan ta det minus 180?
Om du tycker att det är förvirrande med yttervinklar osv så kan följande tillvägagångssätt kanske vara enklare.
Alla trianglar har vinkelsumman 180°
Alla fyrhörningar har vinkelsumman 360°
Det betyder att
15 + 71 + a = 180
71 + a + 160 + b = 360
b + 71 + u = 180
Lös ut a ur första ekvationen, stoppa in i ekvation 2 och lös ut b, stoppa in i ekvation 3 och lös ut u.

Hmmm, jag tror att vi behöver några namn på vinklarna:
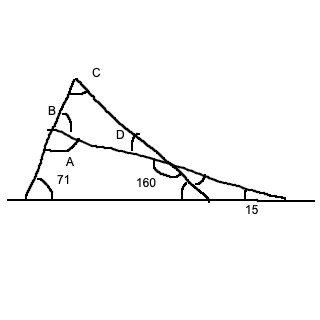
A har vi bestämt till 94 grader. Hur stor är B? På samma sätt som du beräknar B kan du även beräkna D. :)
Yngve skrev:Om du tycker att det är förvirrande med yttervinklar osv så kan följande tillvägagångssätt kanske vara enklare.
Alla trianglar har vinkelsumman 180°
Alla fyrhörningar har vinkelsumman 360°
Det betyder att
15 + 71 + a = 180
71 + a + 160 + b = 360
b + 71 + u = 180
Lös ut a ur första ekvationen, stoppa in i ekvation 2 och lös ut b, stoppa in i ekvation 3 och lös ut u.
Jag tror jag har löst det nu,
15+71+a=180
15+71=86
180-86=94
a=94 grader
71+94+160+b=360
71+94+160=325
360-325=35
b=35 grader
35+71+u=180
35+71=106
180-106=74
u=74
Det bör stämma
Bra, det stämmer.
Räkna gärna även på det andra sättet.
På så sätt vänjer du dig vid att det ofta finns flera olika sätt att lösa ett problem.
Dessutom kan du i en provsituation kolla om svaret verkar rätt: Om du får samma resultat med olika metoder så är sannolikheten stor att svaret är rätt.
Okej, stort tack till alla som hjälpte mig!



