Invers med MacLaurin-Polynom
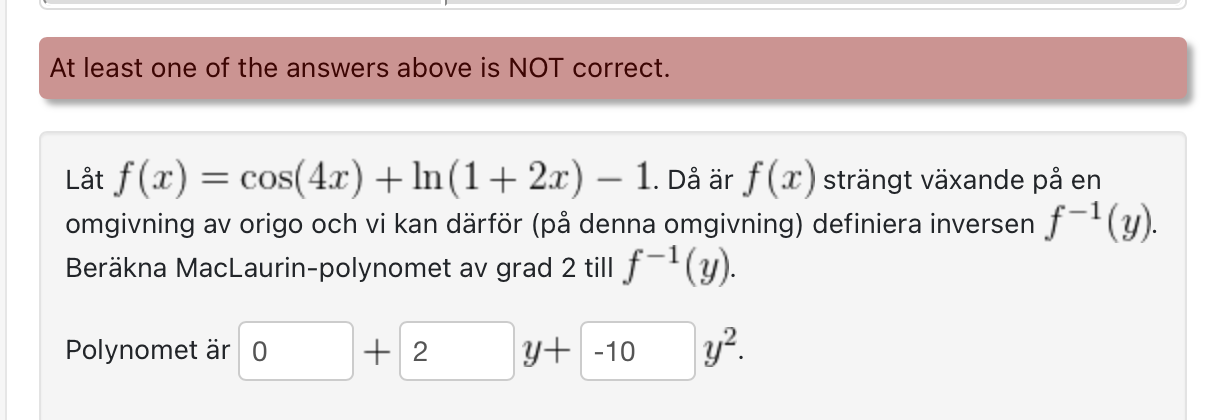
Hej, som uppgiften lydes så ska jag hitta inversen till funktionen, och beräkna MacLaurin-polynomet. Jag kan inte lyckas hitta inversen till funktion genom att byta plats på x och y. Problemet som uppstår är att jag har både cos(4y) och ln(1+2y) som jag ska så till y, kan inte arccos och e samtligt (tror jag iallafall) som att få bort både ln och cos.
Där antar jag att jag ska ta fram MacLaurin-Polynom och därefter ta inversen till polynomet vilket jag har gjort, men får fel svar. Har jag gjort räknefel någon stans? Finns det någon annan metod? Tack!
Lösning nedan:

Eftersom att funktionen f(x) inte är monoton på hela dess definitionsmängd kommer det inte existera någon invers. Därav är det smart att först approximera f med ett polynom när x=0 (där funktionen är strängt monoton) för att sedan hitta inversen av polynomet.
Du har bestämt polynomet till grad 2, men därefter måste du hitta inversen till polynomet. Det räcker inte med att bara ersätta x med y som du gör.
Man kan även utnyttja att det skall gälla att
f-1(f(x)) = x.
Vi kan derivera detta map x.
Df-1(f(x))Df(x) = 1, dvs Df-1(f(x)) = 1/Df(x).
Vi deriverar en gång till
D2f-1(f(x))(Df(x))2 + Df-1(f(x))D2f(x) = 0, dvs D2f-1(f(x)) = -Df-1(f(x))D2f(x)/(Df(x))2.
Sedan vet du från din serieutveckling (om du gjort rätt) att
f(0) = 0
Df(0) = 2
D2f(0) = -20.
Utnyttja sedan detta för att beräkna
f-1(0)
Df-1(0)
D2f-1(0),
och ställ upp Maclaurin av grad 2.
Hur har det gått?
Laguna skrev:Hur har det gått?
Har skrivit av sambandet, men förstår inte hur jag ska komma vidare.

f-1(f(x)) = x. Sätt in x = 0 och utnyttja att f(0) = 0.
Df-1(f(x)) = 1/Df(x). Sätt in x = 0 och utnyttja att f(0) = 0 och Df(0) = 2.
Osv.
PATENTERAMERA skrev:f-1(f(x)) = x. Sätt in x = 0 och utnyttja att f(0) = 0.
Df-1(f(x)) = 1/Df(x). Sätt in x = 0 och utnyttja att f(0) = 0 och Df(0) = 2.
Osv.
Jag har fått fram att . Har jag gjort rätt, bild nedan.

Ja Df-1(0) = 1/2 och f-1(0) = 0.
PATENTERAMERA skrev:Ja Df-1(0) = 1/2 och f-1(0) = 0.
Sedan får jag att $$D^{-1}(0)=1/20. Stämmerdet? Bilden nedan
Alltså blir mitt svar 0+y/2+y^2/20. Men den säger att det är fel svar. Jag testa att räkna om taylor polynom och se om det var där som det blev fel

Philip22 skrev:PATENTERAMERA skrev:Ja Df-1(0) = 1/2 och f-1(0) = 0.
Sedan får jag att $$D^{-1}(0)=1/20. Stämmerdet? Bilden nedan
Alltså blir mitt svar 0+y/2+y^2/20. Men den säger att det är fel svar. Jag testa att räkna om taylor polynom och se om det var där som det blev fel
Här räknas om allt och får 0+y/2 + 5y/2. Fortsatt fel svar. Uträkning nedan:

D2f(0) = -20.
Df(0) = 2.
Df-1(0) = 1/2 = 1/Df(0).
D2f-1(0) = -D2f(0)/(Df(0))3 = -(-20)/23 = 20/8 = 5/2.
f-1(x) = x/2 + (5/4)x2 + O(x3).
Vi kan se om vi kan få samma uttryck genom direkt invertering.
x = f(y) 2y - 10y2 om och endast om f-1(x) = y. Så vi försöker lösa ut y ur uttrycket x = 2y - 10y2.
Vi får en andragradare med lösningen y = (1 - )/10 =
x/2 + (5/4)x2 + O(x3).
PATENTERAMERA skrev:D2f(0) = -20.
Df(0) = 2.
Df-1(0) = 1/2 = 1/Df(0).
D2f-1(0) = -D2f(0)/(Df(0))3 = -(-20)/23 = 20/8 = 5/2.
f-1(x) = x/2 + (5/4)x2 + O(x3).
Vi kan se om vi kan få samma uttryck genom direkt invertering.
x = f(y) 2y - 10y2 om och endast om f-1(x) = y. Så vi försöker lösa ut y ur uttrycket x = 2y - 10y2.
Vi får en andragradare med lösningen y = (1 - )/10 =
x/2 + (5/4)x2 + O(x3).
Tusen tack PanataMera! Rätt svar. Lyckades nu härleda och få rätt på andra derivatan för inversen. Bilden nedan:

Philip22 skrev:PATENTERAMERA skrev:D2f(0) = -20.
Df(0) = 2.
Df-1(0) = 1/2 = 1/Df(0).
D2f-1(0) = -D2f(0)/(Df(0))3 = -(-20)/23 = 20/8 = 5/2.
f-1(x) = x/2 + (5/4)x2 + O(x3).
Vi kan se om vi kan få samma uttryck genom direkt invertering.
x = f(y) 2y - 10y2 om och endast om f-1(x) = y. Så vi försöker lösa ut y ur uttrycket x = 2y - 10y2.
Vi får en andragradare med lösningen y = (1 - )/10 =
x/2 + (5/4)x2 + O(x3).
Tusen tack PanataMera! Rätt svar. Lyckades nu härleda och få rätt på andra derivatan för inversen. Bilden nedan:
PantaMera du får andra derivata för invensen till 5/2.
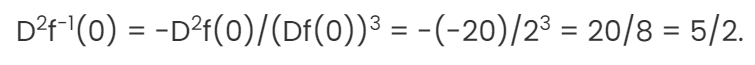
Hur kommer det sig att när det sätts in i polynomen att det blir 5/4?
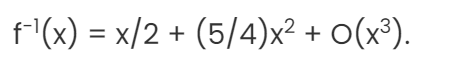
Tänker vi att x^2 / 2!?
Maclaurin. En halva kommer till i Maclaurinformeln.
f-1(x) = f-1(0) + Df-1(0)x + (1/2)D2f-1(0)x2 + O(x3)
Jag tycker det borde gå bra att ansätta y = ax+bx2 och sätta in i uttrycket för x.
OK, någonting så här?
f(f-1(x)) = x.
f(x) = 2x - 10x2 + O(x3).
f-1(x) = ax + bx2 + O(x3). Ansats.
x = 2(ax + bx2) - 10(ax + bx2)2 + O(x3).
(1 - 2a)x + (10a2 - 2b)x2 = O(x3) => 1 - 2a = 0 och 10a2 - 2b = 0 => a = 1/2 och b = 5/4.
Utmärkt. Då har vi fått samma svar med tre olika metoder.




