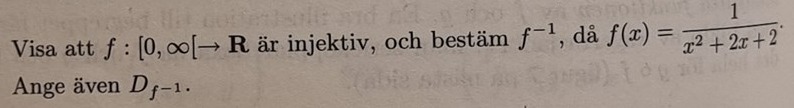Invers funktions definitionsmängd
Hej
Jag har den här upg
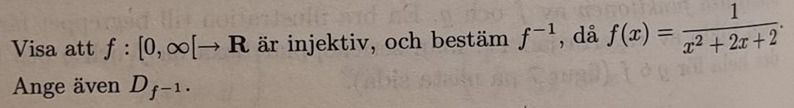
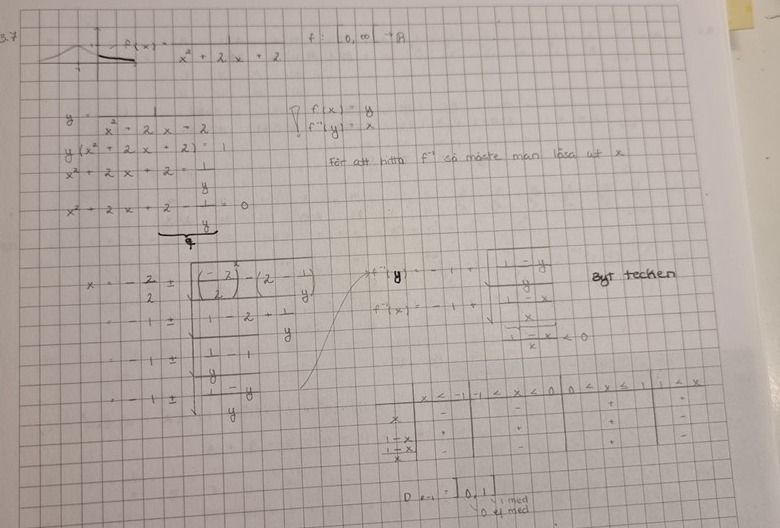
Och fick den här lösningen av min lärare
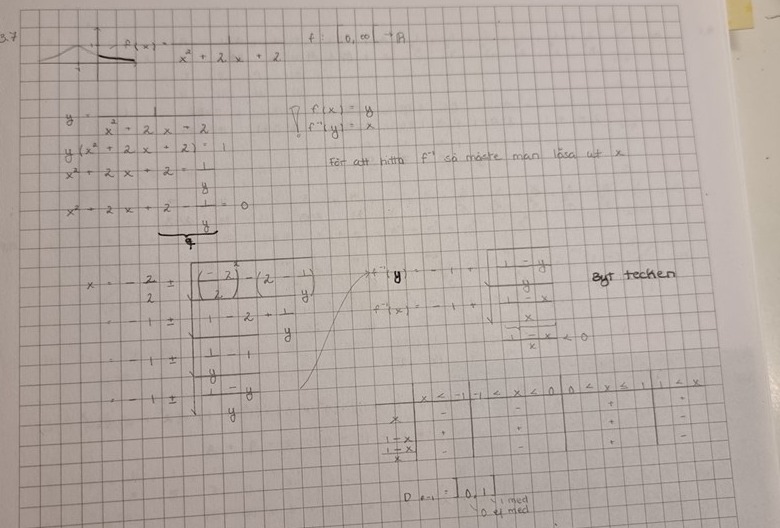
Men jag förstår inte tabellen. Hur får jag fram de värdena? Och hur tolkar jag de värdena så jag får ]0,1]?
Heocon skrev:Hej
Jag har den här upg
Och fick den här lösningen av min lärare
Men jag förstår inte tabellen. Hur får jag fram de värdena? Och hur tolkar jag de värdena så jag får ]0,1]?
Är du med på vad f-1 är?
Borde det inte bli ]0, 1/2]?
Det där är ett intervall, inte en funktion.
Vet du vad som menas med f-1?
PATENTERAMERA skrev:Borde det inte bli ]0, 1/2]?
Det är korrekt.
Tillägg: 22 aug 2024 08:46
är såklart relationen och
F-1 är invers och den vet jag hur man hittar. I vanliga fall brukar funktionen vara enkla så jag kan rita och se definitionsmängden, men här ser jag inte direkt hur funktionen ska se ut för den inversa
Fattar inte de värdena i tabellen dock://
Det verkar som det blivit lite fel i facit.
f-1(x) = -1 + .
Sedan så måste f-1(x) alltid ligga i Df, vilket ger villkor på x. Speciellt så måste f-1(x) vara större än eller lika med 0.
Det betyder att , vilket implicerar att 0 < x 1/2.
Så Df-1 = ]0, 1/2].
Om vi sätter g(x) = x2 + 2x + 2 = (x+1)2 + 1.
g(x) är positiv och strikt ökande då x > -1.
Det betyder att f(x) = 1/g(x) är positiv och strikt avtagande då x 0. Och således är f injektiv.
Det största värdet på f(x) erhålls då x är så litet som möjligt dvs då x = 0. f(0) = 1/2.
f(x) är alltid större än noll men det går att komma godtyckligt nära noll eftersom f(x) går mot noll då x går mot oändlighet.
Så värdemängden för f är ]0, 1/2], vilket borde vara definitionsmängden för inversen.
Tillägg: 22 aug 2024 21:59
Egentligen är det väl så att en funktion måste vara både injektiv och surjektiv för att en invers skall existera. Om en funktion är injektiv så kan man göra den surjektiv genom att krympa målmängden till värdemängden. Inversen är då en funktion från värdemängden till Df.
Från Wikipedia:

PATENTERAMERA skrev:Det verkar som det blivit lite fel i facit.
f-1(x) = -1 + .
Sedan så måste f-1(x) alltid ligga i Df, vilket ger villkor på x. Speciellt så måste f-1(x) vara större än eller lika med 0.
Det betyder att , vilket implicerar att 0 < x 1/2.
Så Df-1 = ]0, 1/2].
Om vi sätter g(x) = x2 + 2x + 2 = (x+1)2 + 1.
g(x) är positiv och strikt ökande då x > -1.
Det betyder att f(x) = 1/g(x) är positiv och strikt avtagande då x 0. Och således är f injektiv.
Det största värdet på f(x) erhålls då x är så litet som möjligt dvs då x = 0. f(0) = 1/2.
f(x) är alltid större än noll men det går att komma godtyckligt nära noll eftersom f(x) går mot noll då x går mot oändlighet.
Så värdemängden för f är ]0, 1/2], vilket borde vara definitionsmängden för inversen.
Tillägg: 22 aug 2024 21:59
Egentligen är det väl så att en funktion måste vara både injektiv och surjektiv för att en invers skall existera. Om en funktion är injektiv så kan man göra den surjektiv genom att krympa målmängden till värdemängden. Inversen är då en funktion från värdemängden till Df.
Wow okej tack🥹🥹