Intressant, enkelt kortspel - jämnt eller udda? (Matematik/Allmänna diskussioner)

Alltid riskabelt att riskera sitt anseende på kombinatorik och sannolikhet, men hoppas jag fattat reglerna rätt.

Leken har 28 jämna och 24 udda kort

Sh (sannolikheten) att korten har samma valör är 3/51 = 1/17.

Fall 1: Sh att du får udda är 6/13. I så fall ser man direkt att du bör gissa att huset får jämnt, dvs udda summa; sh för det är 28/51.

Totalt (6*28) / (13 * 51).

Fall 2: Sh att du får jämnt är 7/13. I så fall är sh att huset får jämnt av annan valör 24/51 och att det får udda 24/51.

Oavsett om du gissar jämn eller udda summa vinner du med sh 7/13 * 24/51.

Totalt är din vinstchans (6*28 + 7*24) / (13*51) = 112 / 221

Koll: Sh att huset vinner är 6/13 * 23/51 + 7/13 * 27/51 = 109/221

Om jag tänkt rätt bör, inför varje parti, du lägga 112 dukater och huset 109 dukater i potten, winner takes it all. Då är spelet rättvist.

Vad är ditt resultat?

Jag håller med!

Jag missade att tänka på att sannolikheten att spelaren får ett jämnt kort inte är detsamma som att denne får ett udda kort (räknade med att sannolikheterna var desamma), men efter en korrigering får jag samma svar som du.

Snyggt!

Tillägg: 16 apr 2025 01:14

Tänk om vi gör en modifiering nu... Låt säga att huset delar ut det första kortet till sig själv, och det andra kortet till spelaren, med resterande regler oförändrade. Hur förändras vinstchanseran då?

naytte skrev

Tillägg: 16 apr 2025 01:14

Tänk om vi gör en modifiering nu... Låt säga att huset delar ut det första kortet till sig själv, och det andra kortet till spelaren, med resterande regler oförändrade. Hur förändras vinstchanseran då?

Hmm, jag är inte med. Det spelar väl ingen roll i vilken ordning de får korten?

Jag kan gissa att summan är udda redan innan vi börjar dela ut kort. Min sannolikhet att vinna är likafullt 112/221.

Det stämmer! Insåg det först efter att jag gjorde beräkningen igen.

Är tydligen för trött för sannolikhet just nu...

Jag får däremot konstiga resultat nu när jag simulerar vidare. Återkommer imorgon efter lite sömn.

naytte skrev:
Jag får däremot konstiga resultat nu när jag simulerar vidare. Återkommer imorgon efter lite sömn.

Även en simulant kan bli trött. Problemet är väldigt väl lämpat för ett sannolikhetsträd.

Jag är också lite fundersam till dina beräkningar i #2. Om man bara räknar på sannolikheten att två slumpvis dragna kort har en jämn eller udda summa så får man också 109/221 respektive 112/221. Man får alltså detta svar utan att ta hänsyn till parregeln, där huset vinner direkt.

När jag simulerar att spelaren gissar på "jämn summa" hela tiden får jag vinstchansen $43.\!4\;\%$ över en miljon simuleringar:

Scriptet som jag använder

from Cards import Deck


def distribute_cards():
    total_games = 1000000
    win = 0
    loss = 0

    for _ in range(total_games):
        deck = Deck().shuffle()  # Blandar en lek med 52 kort

        # Poppar kort 1 & 2
        card1 = deck.pop()
        card2 = deck.pop()

        # Hämtar kortens valörer
        val1 = card1.get_card_value()
        val2 = card2.get_card_value()

        if val1 == val2:
            loss += 1  # Huset vinner automatiskt om det blir par
        elif (val1 + val2) % 2 == 0:
            win += 1   # Spelaren gissar jämnt
        else:
            loss += 1  # Eftersom spelaren gissar jämnt förlorar han om summan blir udda

    probability_of_win = (win / total_games) * 100
    print(f"Probability of player winning: {probability_of_win:.2f}%")


if __name__ == "__main__":
    distribute_cards()

Sannolikheten att två kort med en jämn summa är ett par borde väl vara:

$\displaystyle \frac{\binom{7}{1}\binom{4}{2}+\binom{6}{1}\binom{4}{2}}{\binom{28}{2}+\binom{24}{2}}=\frac{13}{109}$

Så sannolikheten att två kort med jämn summa inte utgör ett par borde vara:

$\displaystyle 1-\frac{13}{109}=\frac{96}{109}$

Summa summarum borde vinstchansen om man alltid gissar jämn summa alltså vara:

$\displaystyle P\left(\text{vinst}\right)=P\left(\text{jämn summa}\right)\cdot P\left(\text{inte par}|\text{jämn summa}\right)=\frac{109}{221}\cdot\frac{96}{109}=\frac{96}{221}\approx43.\!34\; \%$

Detta stämmer ganska bra överrens med det empiriska resultatet (om jag nu har gjort mitt script rätt...)

Jag börjar med att gissa jämn summa.

Fall 1 Sh jag får jämnt kort är 7/13.

Sh att huset isåfall får jämnt som inte är par är 24/51.

Fall 2 Sh att jag får udda kort är 6/13.

Sh att huset får udda som inte är par är 20/51.

Så sh att jag vinner är (7*24+6*20)/(13*51) = 96/221 ≈ 0,434

Så gissar jag jämnt är sh för vinst 96/221, gissar jag udda är sh för vinst 112/221.

Så sant!

Det stämmer också med min simulering. Så det bästa beslutet är med andra ord alltid att gissa på udda summa, då vinner man alltid i längden.

Det som förvirrade var att sannolikheten att summan blir udda är densamma som vinstchansen om man gissar på udda...

naytte skrev:
Jag är också lite fundersam till dina beräkningar i #2. Om man bara räknar på sannolikheten att två slumpvis dragna kort har en jämn eller udda summa så får man också 109/221 respektive 112/221. Man får alltså detta svar utan att ta hänsyn till parregeln, där huset vinner direkt.

När jag simulerar att spelaren gissar på "jämn summa" hela tiden får jag vinstchansen $43.\!4\;\%$ över en miljon simuleringar:
Scriptet som jag använder
from Cards import Deck


def distribute_cards():
    total_games = 1000000
    win = 0
    loss = 0

    for _ in range(total_games):
        deck = Deck().shuffle()  # Blandar en lek med 52 kort

        # Poppar kort 1 & 2
        card1 = deck.pop()
        card2 = deck.pop()

        # Hämtar kortens valörer
        val1 = card1.get_card_value()
        val2 = card2.get_card_value()

        if val1 == val2:
            loss += 1  # Huset vinner automatiskt om det blir par
        elif (val1 + val2) % 2 == 0:
            win += 1   # Spelaren gissar jämnt
        else:
            loss += 1  # Eftersom spelaren gissar jämnt förlorar han om summan blir udda

    probability_of_win = (win / total_games) * 100
    print(f"Probability of player winning: {probability_of_win:.2f}%")


if __name__ == "__main__":
    distribute_cards()
Sannolikheten att två kort med en jämn summa är ett par borde väl vara:

$\displaystyle \frac{\binom{7}{1}\binom{4}{2}+\binom{6}{1}\binom{4}{2}}{\binom{28}{2}+\binom{24}{2}}=\frac{13}{109}$

Så sannolikheten att två kort med jämn summa inte utgör ett par borde vara:

$\displaystyle 1-\frac{13}{109}=\frac{96}{109}$

Summa summarum borde vinstchansen om man alltid gissar jämn summa alltså vara:

$\displaystyle P\left(\text{vinst}\right)=P\left(\text{jämn summa}\right)\cdot P\left(\text{inte par}|\text{jämn summa}\right)=\frac{109}{221}\cdot\frac{96}{109}=\frac{96}{221}\approx43.\!34\; \%$

Detta stämmer ganska bra överrens med det empiriska resultatet (om jag nu har gjort mitt script rätt...)

För oss fåtal dinosaurier som överlevde... vilket programmeringsspråk är detta? Python?

Ja, det är Python!

Grejen är att om det är par så är summan aldrig udda (ja du har redan sett det)

(eftersom u+u = j+j = j).

Därför är det oförmånligt att gissa jämn summa, du kan gissa rätt, men förlorar likafullt.

Yes, snyggt!

Nu har jag en modifikation som påverkar oddsen. Låt säga att spelaren istället får två kort, medan huset fortfarande får ett kort:

Spelaren gör en gissning om summans paritet (alltså summan av valörerna på de två egna korten och husets ena kort)
Om spelarens hand utgör ett par i sig så vinner spelaren automatiskt, oavsett vad huset har för kort och oavsett gissning.
Om något kort i spelarens hand utgör ett par med husets kort så vinner huset, oavsett vad spelaren gissar

Vem är det nu som har bäst vinstchanser?

Men om spelare och hus får triss, vem vinner då?

Då vinner spelaren eftersom hans hand utgör ett par i sig. Ordningen jag skrev upp punkterna i tänker jag är "viktigheten" i kriterierna eller vad man ska säga.

Spelaren gissar pariteten
Om spelaren har ett par själv ==> spelaren vinner oavsett gissning och oavsett vad huset hade
Om spelaren inte hade par själv men det kan bildas ett par mellan något av spelarens kort och husets kort ==> huset vinner
Om inget av de två ovanstående kriterierna uppfylls vinner spelaren om han gissar pariteten rätt, och förlorar om han gissar fel

Men det blir ett svinkrångligt träd, om man inte kan förenkla är det inte matematik.

Har också förgäves försökt lösa det analytiskt en stund nu. Komplexiteten ökade tydligen extremt fort med den lilla förändringen. 😅

"Empiriskt" så ligger chansen för vinst om man gissar jämn på ca. 46.4 %, och chansen för vinst på ca. 48.1 % om man gissar udda.

PS min burk hängde sig, därför jag var seg med svaret.

Jag ser inte att det är svårare än det förra problemet. Egentligen. Men för eller senare gör man ett slarvfel och då är man lost.

Det är 52*51*50 permutationer av de tre första korten, det gäller att få ihopp just så mänga disjunkta utfall.

Jo men precis. Det är ju delvis detta som gör spel som Blackjack så himla krångliga att lösa analytiskt också (tror inte ens att det har gjorts). Det finns så många fall att ta hänsyn till att det blir nästan omöjligt.

, se nästa post

Jo men det gick till sist!

Sätt 52*51*50 = N

Då fås sh att du vinner med eget par = 7800/N

Sh att huset parar med din hand = 14976/N

Sh att summan udda utan par = 56064/N

Sh att summan jämn utan par = 53760/N

Jag tar bort förra bilden, diverse slarvfel där.

Jag tänkte på det, om du får dina två kort, så bör oddset för jämn eller udda totalsumma påverkas av huruvida du tittar på J+J, J+U eller U+U. Men den analysen får vila till senare. I din presentation av problemet tolkar jag det som att man satsar innan man sett sina egna kort (rimligt iofs, när du ser dina kort vet du om du kan plocka hem en direktvinst pga eget par).

Jag får det till:

slh att man får eget par är 1*(3/51).

Om man fått J+J är slh för vinst om man säger "J" (20/50), slh för vinst om man säger "U" (24/50)

Om man fått J+U är slh för vinst om man säger "J" (20/50), slh för vinst om man säger "U" (24/50)

Om man fått U+U är slh för vinst om man säger "J" (28/50), slh för vinst om man säger "U" (16/50)

slh för J+J men inget par är (28/52)*(24/51)

slh för J+U är (28/52)*(24/51)

slh för U+U men inget par är (24/52)*(20/51)

Så sannolikheten för vinst om man spelar optimalt borde bli:

3/51+(28/52)*(24/51)*(24/50)+(28/52)*(24/51)*(24/50)+(24/52)*(20/51)*(28/50)=

3/51+ (1/(52*51*50))*(28*24*24*2+28*24*20)=

3/51+ (28*24*68)/(52*51*50)= 0,4034389140271493...

Huset vinner.

Jag är dock osäker på om jag nu räknat tagit hänsyn till ordningen för J & U, och om jag borde ha gjort det. I sådant fall blir slh för vinst 0,5250678733031674..., dvs huset förlorar.

Jag ska gå ut i solen, men detta kan inte vänta.

Ett realistiskt spel är att du tittar på dina två kort, men huset har inte visat sitt kort.

Ska du gissa att summan av era tre kort är jämn eller udda?

Om vi då räknar bort fallen med par som du inte kan påverka så får jag

1 Du har två udda kort. Gissa på jämn summa, vinstchans 7/11, förlustrisk 4/11.

2 Du har ett eller två jämna kort. Gissa udda summa, vinstch 6/11 förlrisk 5/11.

Det är lurigt med betingade sh. Jag ska göra en översyn när solen gått ner.

Spännande inlägg!

Jag är själv för dålig för att försöka mig på detta analytiskt men jag har precis börjat lära mig om "Q-Learning" och det skulle nog passa perfekt för ett problem som detta. Jag har redan börjat slipa lite på lite kod i Python där jag tänker försöka bygga en modell som hittar den optimala spelstrategin och blir så bra som möjligt över miljontals rundor.

Kanske kan vi få några bra insikter av det! :D

Så här blev det för mig:

Du spelar spelet N = 52!/49! gånger (dvs 52*51*50 = 132600 ggr) med ny permutation av korten varje gång (är man systematisk behöver man inte köra miljontals gånger).

7800 gånger vinner du pga eget par.

14976 ggr vinner huset för att det parar sig med någon av dina valörer.

Jag räknar bort de tillfällena i fortsättningen. u och j betecknar udda resp jämnt kort, U och J betyder udda resp jämn summa.

Då fördelar sig summorna som följer

u+u+u = U: 7680 ggr. u+u+j = J: 13440 ggr

u+j+j el j+u+j = U: 32256 ggr. u+j+u el j+u+u = J: 26880 ggr

j+j+u = U: 16128 ggr j+j+j = J: 13440 ggr

Så ska du gissa innan du sett dina kort så ska du gissa U. Då har du sh

(7680+32256+16128+7800) / N ≈ 63864/132600 ≈ 0,4816 att vinna.

Om du sett dina kort men inte husets så ska du gissa J om du har u+u, i annat fall U.

Då har du sh

(13440+32256+16128+7800)/N = 69624/132600 ≈ 0,5251 att vinna.

PS. Det vore litet kul att se hur snabbt din Pyton/Monte C-metod snävar in mot mina värden.

Har skrivit något som verkar fungera, och nu efter några miljoner iterationer ligger vinstchansen i snitt på typ 49 %, alltså högre än om man bara gissar jämn/udda utan att ta hänsyn till sin hand.

Jag återkommer om några dagar när jag har förfinat detta och har tillgång till mer datorkraft. Är på landet nu och har bara min fjuttiga laptop, medan burken hemma sitter på 24 trådar…

Spännande tråd! Detta ger jag mig absolut inte på med p&p, men kanske med c#.

Har ni funderat på (säg) sex stycken kortlekar utan återläggning, med fler spelare som har hyfsat minne? 😅

Jag har funderat på 52 kortlekar. Med ett kort var.

Jag trodde först det var ett enkelt problem, bara rita träddiagram, klart. Och i efterhand känns det inte så märkvärdigt. Men när jag var inne i det, var det krångligare och mer tidskrävande än jag hade trott, ett antal felräkningar på vägen. Sannolikheten betingat av att jag inte har par osv, hänsyn till ordning mm. Jag lärde mig en del på att försöka reda ut det.

Det ser lovande ut, hörni!

Nu efter några miljoner rundor (typ 7 miljoner) har modellens vinstchans stigit till ca. 51 % (körde 1 miljon testrundor med epsilon = 0 och tog genomsnittet):

Din analytiska lösning verkar stämma, @Marilyn! :D

Jag har tränat modellen nu några miljoner gånger (går ganska långsamt så jag skulle tippa på endast 20 milj. hittills) och har extraherat datan modellen har hittills.

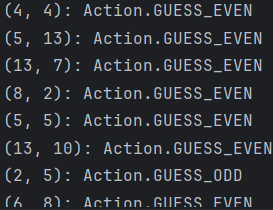
Det verkar som om även din strategi (om när man ska gissa vad) stämmer, @Marilyn! (däremot anser modellen att man har bättre vinstchans om man gissar jämnt med paret (8,2), tror den behöver några miljoner rundor till på sig).

Här är några exempel på den bästa strategin hittills för olika par av kort som spelare (i de fall man har par spelar gissningen givetvis ingen roll):

Tillägg: 19 apr 2025 18:04

Jag tänker visualisera den här datan och återkomma, t.ex. se hur "sant" det är hittills att u+u -> [j är bästa gissningen]

För dokumentationens skull :) Hoppas det blev rätt papper.

Just det, det blev ju mycket enklare! Jäkla betingningar.

Om du sitter med u+u (ej par) så finns det 22 u och 28 j kvar.

Då är sh (vinst om jag gissar summa U) = 16/50

Det ska inte jämföras med sh (förlust om jag gissar U) = 34/50, utan med

sh(vinst om jag gissar J) = 28/50

Om du sitter med u+j eller j+u så är

sh(vinst om du gissar U) = 24/50

sh(vinst om du gissar J) = 20/50

Om du sitter med j+j så är

sh(vinst om du gissar U) = 24/50

sh(vinst om du gissar J) = 20/50

Så har du u+u ska du gissa summa J. I övriga fall ska du gissa U.

I ditt fall (8, 2) så blir det vinst på alla 24 udda kort och förlust på de övriga om du gissar U.

Sh (vinst om du gissar U) = 0,48

Om du gissar J så vinner du på alla j-kort utom 2 och 8 och förlorar på de övriga.

Sh (vinst om du gissar J) = 0,40.

För detta resonemang behöver man inte mitt stora träd och långa beräkningar.

Det luriga är att man gärna ställer

sh(vinst om jag gissar U) mot sh(förlust om jag gissar U).

Men det intressanta för mitt val är

sh(vinst om jag gissar U) mot sh(vinst om jag gissar J).

Nu har jag låtit datorn tugga några miljoner episoder till och har sänkt modellens "learning rate" över tid (för att minimera störningar från slumpen i min data) och det kan nog knappt bli bättre än så här:

EDIT:

VI BÖRJAR NÄRMA OSS :D

Ja, det finns ju flera sannolikheter att beräkna.

Dels ska du avgöra om du ska spela spelet eller inte. Har du mer eller mindre än 50 & chans att vinna?

Om du spelar, så är nästa fråga: ska du gissa på U eller J? Om du gissar innan du sett dina kort så ska du välja U och har i så fall sh 0,4816.att vinna. Om du gissar när du har sett korten så har du redan cashat in en viss matematisk vinst som inte påverkas av din gissning, och du ska göra bästa val av U eller J utifrån korten du tittar på. Det var min sista beräkning – betingat av att du inte tittar på ett par, vad är vinstsh vid val av U eller J?

Som någon matematiker sa, hjärnan är hjälpligt konstruerad för att hantera krångliga problem inom geometri, analys och algebra, men inte ens för skenbart enkla shproblem. Märkligt att en så enkel situation kan bli så krånglig att bena upp. Man måste verkligen formulera premisserna glasklart för den sh man beräknar.

Nu har jag skrivit om min kod en aning och har tränat en modell som är så nära perfekt jag kommer komma med tanke på att slumpen är ganska stor. Den ger följande strategi efter extraherande av data:

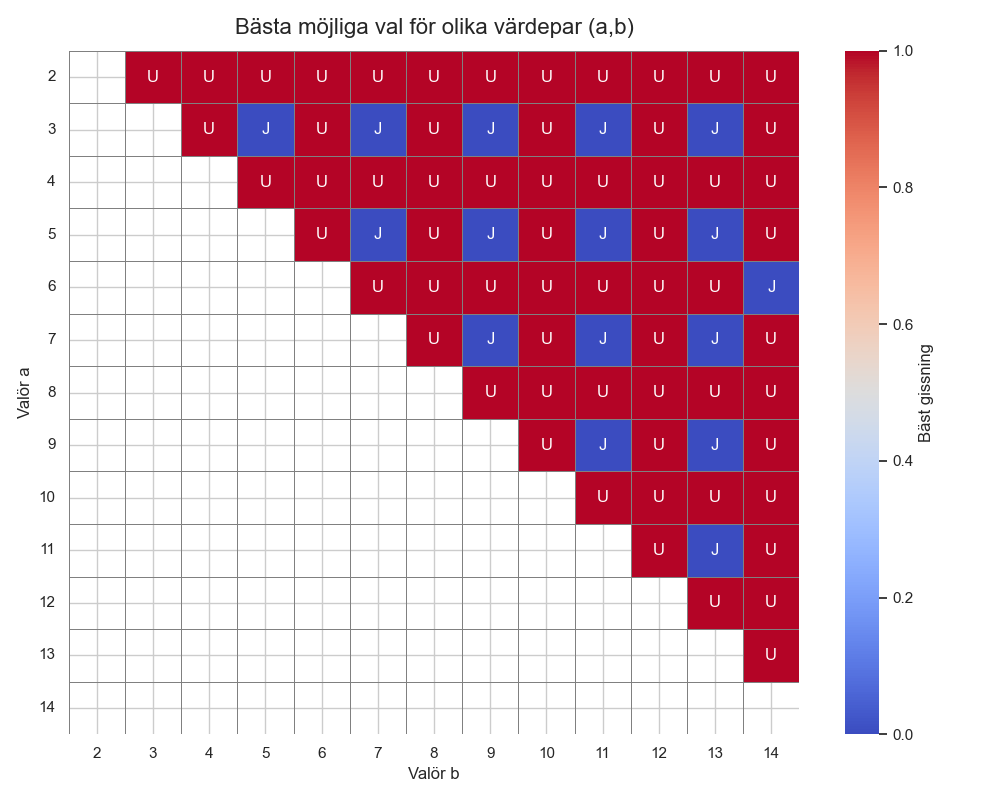
Vi ser en liten anomali vid paret (6, 14) som egentligen borde mappas mot U. Här är för övrigt koden jag har skrivit om någon är intresserad:

Actions.py

from enum import Enum

class Action(Enum):
    GUESS_EVEN = 0
    GUESS_ODD = 1

Cards.py

import random
import enum


class CardSuites(enum.Enum):
    heart = 0x00
    spades = 0x01
    clubs = 0x02
    diamonds = 0x03


class CardValues(enum.Enum):
    val_1 = 1
    val_2 = 2
    val_3 = 3
    val_4 = 4
    val_5 = 5
    val_6 = 6
    val_7 = 7
    val_8 = 8
    val_9 = 9
    val_10 = 10
    val_A = 11
    val_K = 12
    val_Q = 13
    val_Kn = 14


class Card:

    def __init__(self, suite: CardSuites, value: CardValues):
        self.suite: CardSuites = suite
        self.value: CardValues = value

    def get_card_value(self) -> int:
        return self._internal_value_to_card_value()

    def _internal_value_to_card_value(self) -> int:
        if self.value == CardValues.val_10:
            return 10

        if self.value == CardValues.val_Q:
            return 12

        if self.value == CardValues.val_K:
            return 13

        if self.value == CardValues.val_Kn:
            return 11

        if self.value == CardValues.val_A:
            return 14

        return self.value.value

    def __repr__(self):
        val = self._internal_value_to_card_value()
        return "{0} - {1}".format(val, self.suite)



class Deck:

    def __init__(self):
        self.cards = []
        for suite in CardSuites:
            for value in CardValues:
                if value == CardValues.val_1:
                    continue
                self.cards.append(Card(suite, value))

    def shuffle(self):
        shuffled_deck: list[Card] = self.cards.copy()
        random.shuffle(shuffled_deck)
        return shuffled_deck

GameEnvironment.py

from Actions import Action
from Cards import Deck

class GameEnv:
    def __init__(self):
        self.reset()

    def reset(self):
        self.deck = Deck().shuffle()
        self.player_hand = [self.deck.pop(), self.deck.pop()]
        self.dealer_card = self.deck.pop()
        self.reward = 0
        return self._get_observation()

    def _get_observation(self):
        return tuple(card.get_card_value() for card in self.player_hand)

    def step(self, action: Action):

        if self.player_hand[0].get_card_value() == self.player_hand[1].get_card_value():
            self.reward = 2
            return self._get_observation(), self.reward, {"reason: ": "player pair"}

        total = sum(card.get_card_value() for card in self.player_hand + [self.dealer_card])
        is_even = total % 2 == 0

        dealer_val = self.dealer_card.get_card_value()
        player_vals = [card.get_card_value() for card in self.player_hand]

        if dealer_val in player_vals:
            self.reward = -1
            return self._get_observation(), self.reward, {"reason: ": "dealer pair"}

        if (action == Action.GUESS_EVEN and is_even) or (action == Action.GUESS_ODD and not is_even):
            self.reward = 1
            return self._get_observation(), self.reward, {"reason: ": "correct guess"}
        else:
            self.reward = -1
            return self._get_observation(), self.reward, {"reason: ": "incorrect guess"}

Agent.py

import random
from Actions import Action
from collections import defaultdict
import pickle

class QLearningAgent:
    def __init__(self, epsilon = 0.0, alpha = 0.0001): #välj epsilon och alpha efter behov
        self.q_table = defaultdict(lambda: {action: 0.0 for action in Action})
        self.epsilon = epsilon
        self.alpha = alpha

    def choose_action(self, state):
        if random.random() < self.epsilon:
            return random.choice(list(Action))
        else:
            actions = self.q_table[state]
            return max(actions, key=actions.get)

    def learn(self, state, action, reward):
        old_q = self.q_table[state][action]
        new_q = old_q + self.alpha * (reward - old_q)
        self.q_table[state][action] = new_q

    def save_q_table(self, filename="q_table.pkl"):
        with open(filename, "wb") as f:
            pickle.dump(dict(self.q_table), f)

    def load_q_table(self, filename="q_table.pkl"):
        with open(filename, "rb") as f:
            data = pickle.load(f)
            self.q_table = defaultdict(lambda: {action: 0.0 for action in Action}, data)

main.py

from Agent import QLearningAgent
from GameEnvironemnt import GameEnv

env = GameEnv()
agent = QLearningAgent()

try:
    agent.load_q_table()
    print("Loaded saved Q-table")
except FileNotFoundError:
    print("No saved Q-table, starting fresh...")

num_episodes = 1000000
wins = 0

for episode in range(num_episodes):
    state = env.reset()
    action = agent.choose_action(state)
    observation, reward, info = env.step(action)

    if reward > 0:
        wins += 1

    agent.learn(state, action, reward)

agent.save_q_table()
print(f"Win rate: {wins/num_episodes}")

Jag vill även tacka ChatGPT för scriptet för den fina grafiken. Den använde libb jag inte ens visste fanns. Kommer med ett git-repo imorgon.

Tillägg: 21 apr 2025 02:16

Du hade med andra ord helt rätt, @Marilyn. Snyggt!

Marilyn skrev:
Dels ska du avgöra om du ska spela spelet eller inte. Har du mer eller mindre än 50 & chans att vinna?

Om alternativet att välja att inte spela för de givna korten finns är uppgiften superenkel: kontrollera om du har fått ett par eller inte. Om inte: spela inte; om du har ett par: spela. 3/51 av alla rundor kommer du spela och garanterat vinna.

Jag trodde det var tydligt men jag tänker givetvis att man gör sin insats innan man får sina kort.