Intressanta polynom för att definiera "the knight's metric"

Halloj!

Jag har under en längre period funderat på om det är möjligt att definiera någon typ av funktion $N\left(d\right)$ , som med hjälp av ett par av start- och slutrutor på ett schackbräde kan beräkna det minsta antalet drag, $N$ , som en springare behöver för att röra sig mellan dessa. Variabeln $d$ i mitt fall betecknar det euklidiska avståndet mellan två rutor, om man tänker att schackbrädet är ett kartestiskt koordinatsystem.

Jag bestämde mig för några dagar sedan att ta upp projektet igen efter att det legat dött ganska länge eftersom jag är mycket bättre på att programmera nu. Jag har inte löst problemet fullt ut, men jag har nu en funktion $N=N\left(d\right)$ som gäller då $\displaystyle\left\lfloor d \right\rfloor>2$ . Jag ville bara dela med mig av denna funktion:

$\displaystyle N{(d\ge 3)}=\left\{\begin{array}{ll}\frac{(\left\lfloor d \right\rfloor)^{6}}{60}-\frac{37(\left\lfloor d \right\rfloor)^{5}}{60}+\frac{28(\left\lfloor d \right\rfloor)^{4}}{3}-\frac{295(\left\lfloor d \right\rfloor)^{3}}{4}+\frac{6393(\left\lfloor d \right\rfloor)^{2}}{20}-\frac{21499(\left\lfloor d \right\rfloor)}{30}+648,&\Delta x\equiv-\Delta y\;\;\mod2\\frac{(\left\lfloor d \right\rfloor)^{6}}{36}-\frac{59(\left\lfloor d \right\rfloor)^{5}}{60}+\frac{127(\left\lfloor d \right\rfloor)^{4}}{9}-\frac{1259(\left\lfloor d \right\rfloor)^{3}}{12}+\frac{15331(\left\lfloor d \right\rfloor)^{2}}{36}-\frac{8941(\left\lfloor d \right\rfloor)}{10}+761,&\text{annars}\end{array}\right.$

där $d=\sqrt{\Delta x^2+\Delta y^2}$

Är visserligen väldigt klumpigt men jag tyckte det var lite småcoolt så jag ville dela med mig av det. Om någon vill testa det är det bara att köra på! Koordinatsystemet "definieras" enligt:

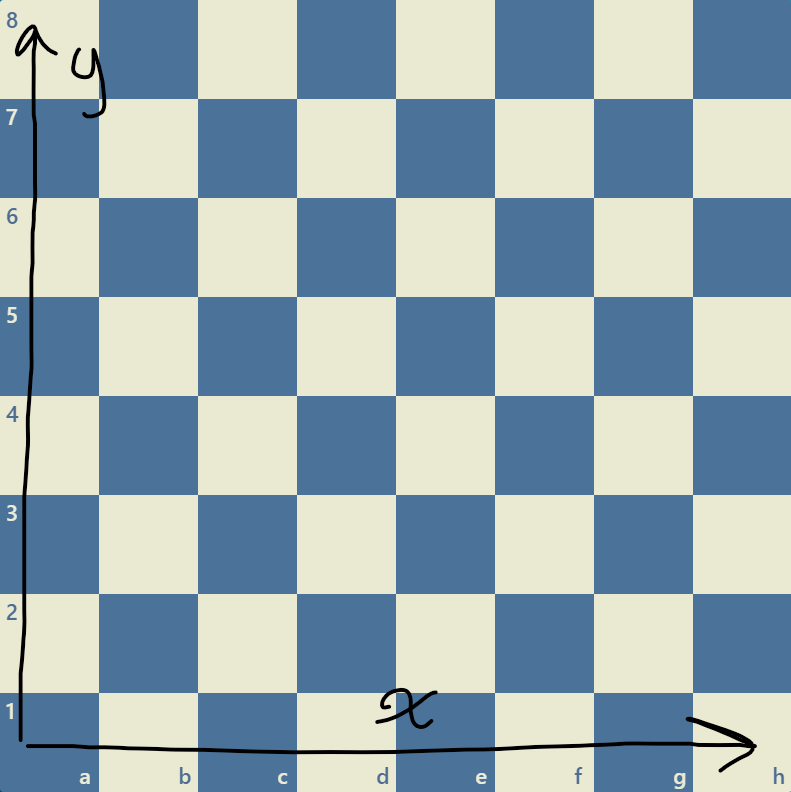
Att säga att $\Delta x \equiv -\Delta y \;\; \mod 2$ är egentligen bara ett sätt att säga att båda rutorna har samma färg. Detta är viktigt eftersom springaren bara kan röra sig till rutor av motsatt färg på ett udda antal drag, och till rutor av samma färg på ett jämnt antal drag.

Hur tänker du kring inputen d?

Varför inte en multivariabel funktion som tar in start och slutposition?

Tillägg: 19 okt 2024 18:40

Roligt projekt för övrigt!

Tillägg: 19 okt 2024 18:45

Misstänker att det enbart är den relativa positionen som spelar roll, och sedan följer resterande av symmetri.

Tänkte att det finns två fall att ha en relativ position på 5 l.e. men insåg nu att de resulterar i lika många steg till målet (3 stycken).

Varför inte en multivariabel funktion som tar in start och slutposition?

Eftersom jag ville ha något enkelt att plotta och tolka. Jag tycker att tredimensionella grafer är ganska svåra och jobbiga att tolka, så om man kan hitta ett enklare samband så vore det att föredra. Det var mest slump att jag kom fram till det här sambandet. Jag satt och plottade några datapunkter i ett Pythonscript jag hade gjort och såg en sak för $\left\lfloor d \right\rfloor > 2$ :

Varje $x$ -koordinat "mappar" till exakt två $y$ -värden, beroende på om antalet drag är jämnt eller udda, vilket i sin tur beror på om rutorna har "samma paritet" $\mod 2$ . Så det fanns inte riktigt någon anledning, bara satt och lekte runt lite och råkade märka detta på i en av mina plots. Sedan anpassade jag bara två lagrangepolynom till datapunkterna, så så värst sofistikerat är detta egentligen inte 😅. Mönstret pajar då brädet är större än 8x8. Här har vi 21x21:

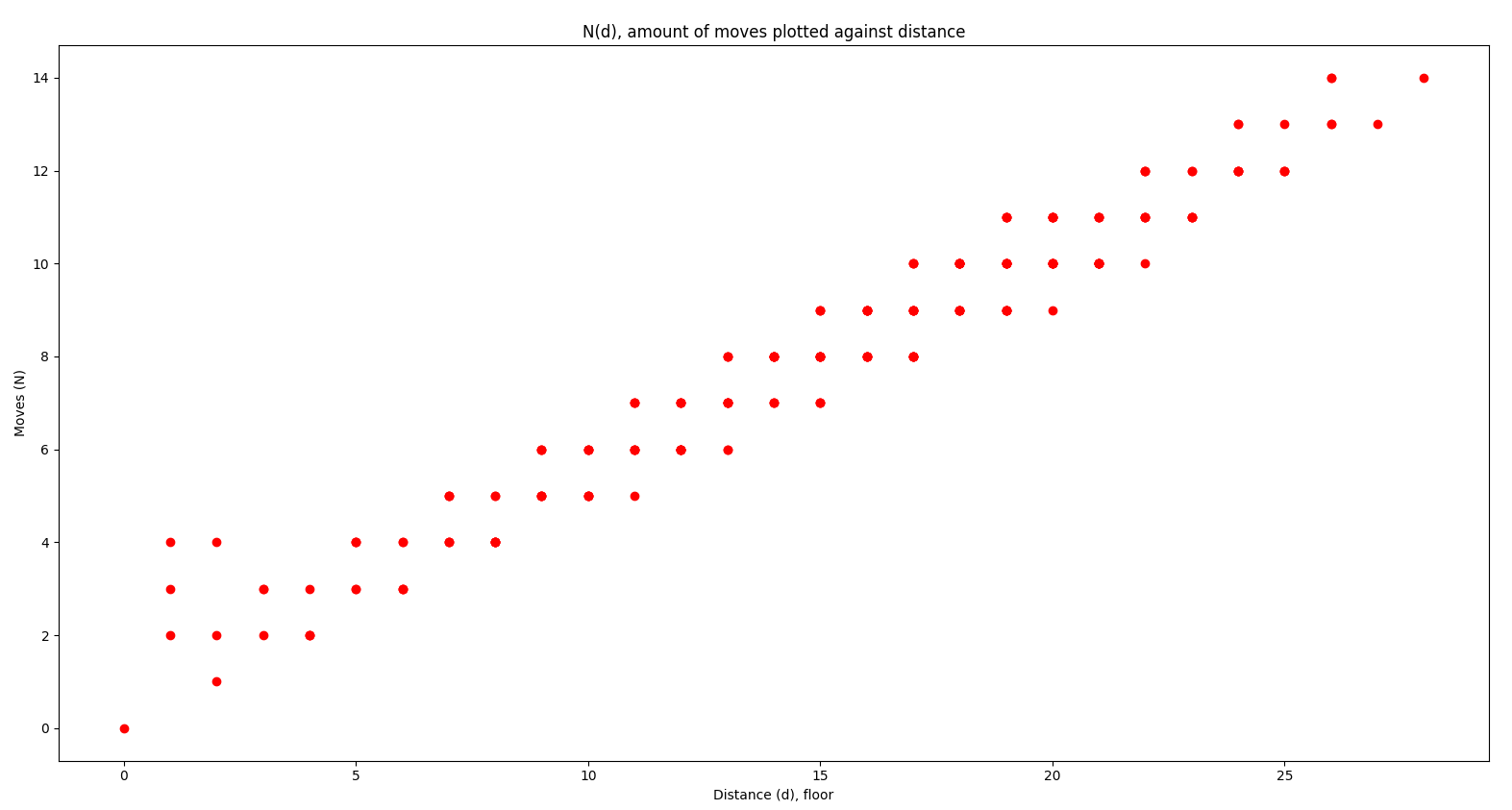
Som du ser har en del $x$ -värden $3$ $y$ -värden. Men jag tänkte på det förut, även här har vi ju udda/jämn-paritet. Kanske kan man kolla paritet mod4 eller mod6 när $\left\lfloor d \right\rfloor$ är stort? Då borde ju $N$ också vara större, och då kan man skilja på vilket av de två möjliga jämna/udda antalen drag det är.

Skulle vara intressant att se vad du får om du skippar floor-funktionen. Plotta helt enkelt datapunkterna för de äkta d-värdena du har.

Plotta dem kan jag, men det finns tyvärr inte något lagrangepolynom eftersom samma värde på d kan ge olika många drag. I den första bilden är brädet 8x8, i den andra 21x21. Ju fler rutor man lägger till, desto fler dubletter kommer man få bland x-koordinaterna. Så lagrange-interpolering funkar inte ordentligt.

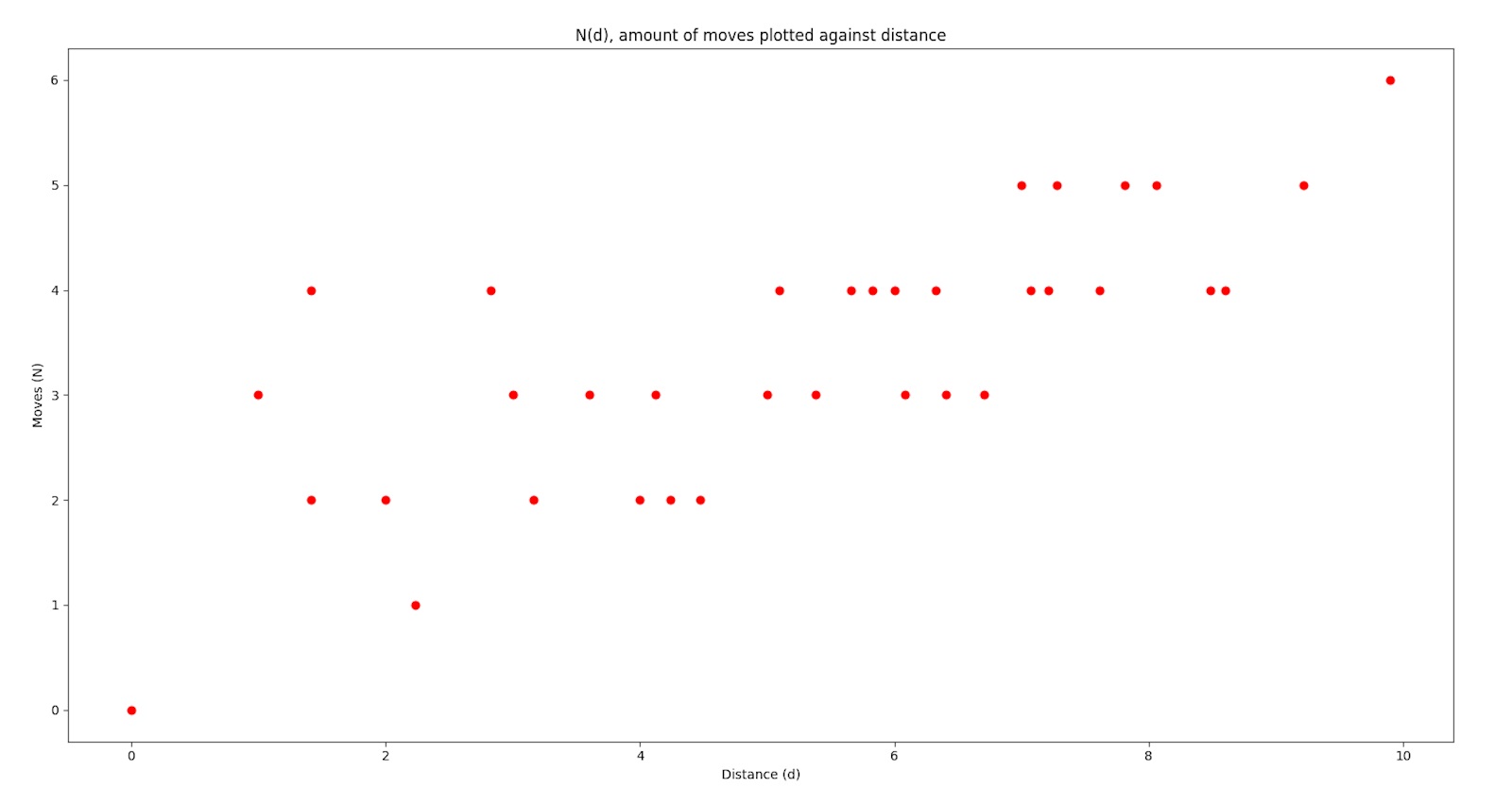
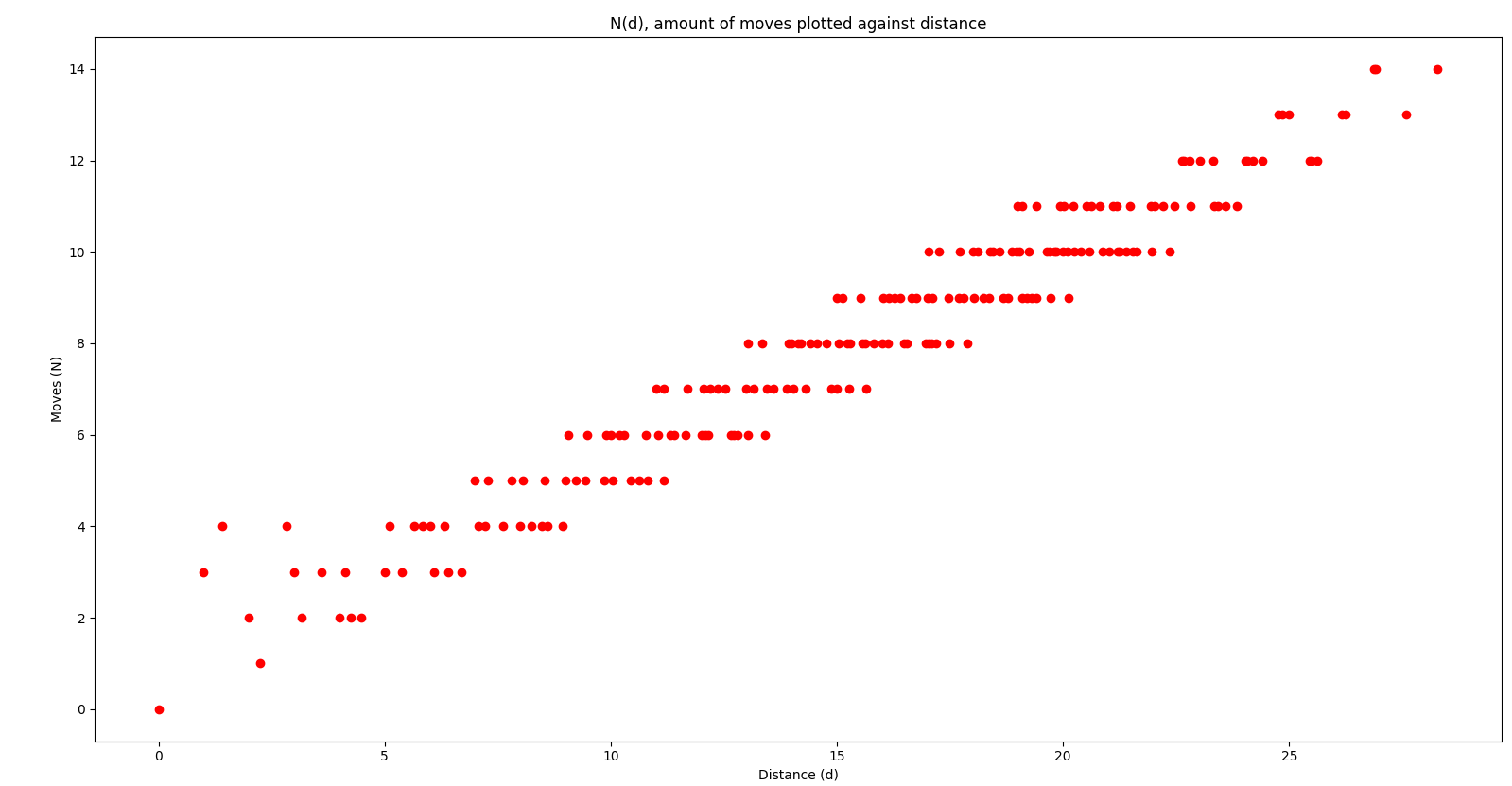
naytte skrev:
Plotta dem kan jag, men det finns tyvärr inte något lagrangepolynom eftersom samma värde på d kan ge olika många drag.

Är du säker på detta? Tycker det ser ut som att varje d ger precis ett värde på N. Dessutom om du funderar lite på det bör det inte vara många rörelser som ger samma värde på d (enda jag kan komma på är om du rör dig 5 rutor rakt eller 4 rakt och 3 och sidan, båda dessa ger samma d men också samma N så det skapar inga problem).

Kom ihåg också att du alltid kan anpassa ett polynom till ett gäng punkter, sålänge polynomet har tillräckligt hög grad.

Är du säker på detta?

Ja, det kan vara svårt att se men någonstans i röran finns det ett $d$ som ger flera $N$ . Även i början finns det ett:

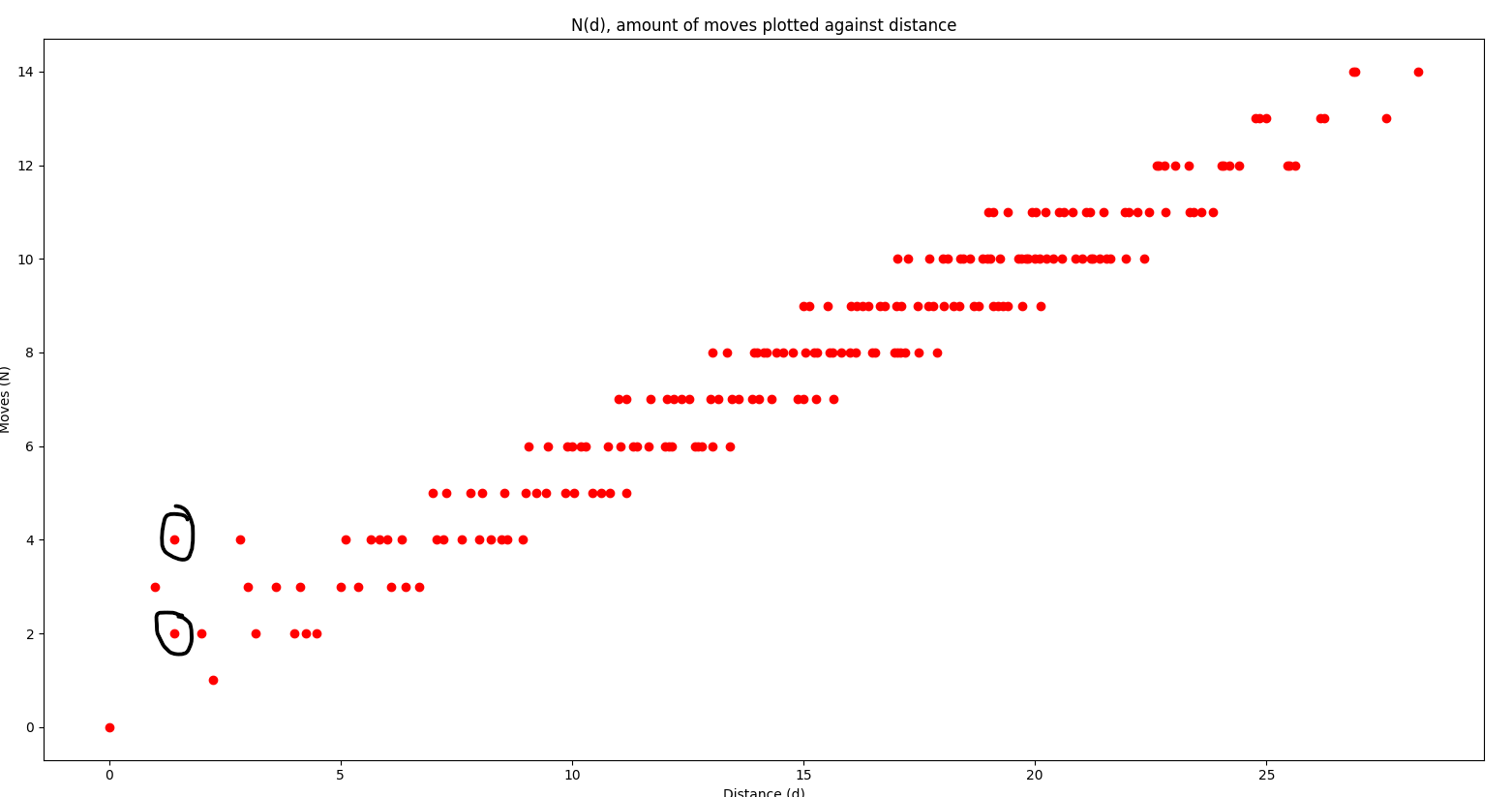
Anledningen till att dessa två punkter inte fanns med i min tidigare bild var att jag manuellt hade tagit bort dem för att testa om jag kunde interpolera ett lagrangepolynom då, och glömt ändra tillbaka det. "Anomalin" i början uppträder vid $d=\sqrt{2}$ .

Kom ihåg också att du alltid kan anpassa ett polynom till ett gäng punkter, sålänge polynomet har tillräckligt hög grad.

Det jag har kört på hittills är lagrangeinterpolation, men känner du till andra metoder som kanske skulle funka bättre? Jag får ett ganska konstigt beteende på mitt lagrangepolynom för vissa datamängder, trots att mappningen $d \mapsto N(d)$ bara mappar ett $d$ till exakt ett $N$ .

Hur har du tagit fram datapunkterna? Jag inser nu att problemet är lite större än vad jag först uppfattade det som. Beroende på var man startar och slutar kan man inte tala alla möjliga vägar (startar vi nära ett hörn försvinner ca 75% av de möjliga vägarna). Detta leder förmodligen till att samma värde på d kan ge olika svar.

En komplett analys hade kunnat göras om du skapade en funktion som tar in 2 värden (alternativt 4), där värden är startpunkt och slutpunkt (alternativt 2 värden för startpunkt och 2 värden för slutpunkt). Men det kanske är ett projekt för en annan dag.

Jag har inga bättre förslag tyvärr. När jag har jobbat med det där använde jag någon inbyggd funktion i Matlab. Jag gissar att alla metoder ger likvärdiga resultat.

Svara

Visa senaste svar