Intergral till (tanx)^3

Nu har jag inte försökt lösa den, men det ser väldigt lovande ut att ansätta $u = 1 - \sin^2 x$. Skriv om nämnaren som $\cos x (1-\sin^2 x)$ så ser du nog varför.

EDIT: jag kunde inte hålla mig från att lösa den. Så här hade jag gjort:

$\displaystyle \int_{}^{}\tan^3 x\mathrm{d}x=\int_{}^{}\frac{\sin^3 x}{\cos^3 x}\mathrm{d}x = \int_{}^{}\frac{\sin^3 x }{\cos x(1-\sin^2 x)}\mathrm{d}x$

Låt vidare $\displaystyle u = 1-\sin^2 x \implies \mathrm{d}u = -2\sin x \cos x \mathrm{d}x$.

Vi förlänger nu med $-2\cos x$ i både nämnare och täljare och erhåller:

$\displaystyle -\frac{1}{2}\int_{}^{}\frac{-2\sin^3x\cos x}{\cos^2 x(1-\sin^2 x)}\mathrm{d}x=-\frac{1}{2}\int_{}^{}\frac{\sin^2 x}{\cos^2 x(1-\sin^2 x)}\mathrm{d}u=-\frac{1}{2}\int_{}^{}\frac{u+1}{u^2}\mathrm{d}u$

$\displaystyle =\frac{1}{2}\left( \frac{1}{u}-\ln u\right)+C=\frac{\sec^2 x}{2}-\ln\cos x+C$

naytte skrev:

Nu har jag inte försökt lösa den, men det ser väldigt lovande ut att ansätta $u = 1 - \sin^2 x$. Skriv om nämnaren som $\cos x (1-\sin^2 x)$ så ser du nog varför.

EDIT: jag kunde inte hålla mig från att lösa den. Så här hade jag gjort:

$\displaystyle \int_{}^{}\tan^3 x\mathrm{d}x=\int_{}^{}\frac{\sin^3 x}{\cos^3 x}\mathrm{d}x = \int_{}^{}\frac{\sin^3 x }{\cos x(1-\sin^2 x)}\mathrm{d}x$

Låt vidare $\displaystyle u = 1-\sin^2 x \implies \mathrm{d}u = -2\sin x \cos x \mathrm{d}x$.

Vi förlänger nu med $-2\cos x$ i både nämnare och täljare och erhåller:

$\displaystyle -\frac{1}{2}\int_{}^{}\frac{-2\sin^3x\cos x}{\cos^2 x(1-\sin^2 x)}\mathrm{d}x=-\frac{1}{2}\int_{}^{}\frac{\sin^2 x}{\cos^2 x(1-\sin^2 x)}\mathrm{d}u=-\frac{1}{2}\int_{}^{}\frac{u+1}{u^2}\mathrm{d}u$

$\displaystyle =\frac{1}{2}\left( \frac{1}{u}-\ln u\right)+C=\frac{\sec^2 x}{2}-\ln\cos x+C$

Där är något teckenfel, men annars en fin lösning.

Japp, insåg det nu också och letar förgäves efter det... Börjar stirra mig blind nu så säg gärna till om du hittar det så redigerar jag inlägget!

naytte skrev:

Japp, insåg det nu också och letar förgäves efter det... Börjar stirra mig blind nu så säg gärna till om du hittar det så redigerar jag inlägget!

sin^2(x)=1-u

Attans! 

Nu har det tyvärr gått för lång tid för att jag ska kunna redigera inlägget, men förhoppningsvis blev @Miss Smarthead hjälpt ändå!

naytte skrev:

$\displaystyle =\frac{1}{2}\left( \frac{1}{u}-\ln u\right)+C=\frac{\sec^2 x}{2}-\ln\cos x+C$

Tack så mycket! Kommit en bra bit på väg nu, två frågor bara.

1. Får man kombinera "du" med x som du gjort?

2. Hänger inte riktigt med vad som händer i sista steget. Antar att det skall stå ln(cos^2(x)) men var kommer sec delen från?

1. Får man kombinera "du" med x som du gjort?

Japp, varför skulle man inte få det? $\mathrm{d}u$ är bara ett tal.

2. Hänger inte riktigt med vad som händer i sista steget. Antar att det skall stå ln(cos^2(x)) men var kommer sec delen från?

Nej, det ska stå $\ln(\cos x)$. Faktorn 1/2 framför är samma som att ta roten ur på argumentet. $\sec x$ är detsamma som $1/\cos x$. Och vi visste ju att $u = 1-\sin^2 x = \cos^2 x$.

Miss Smarthead skrev:

Jag har verkligen fastnat på den här uppgiften. Här är en bild på en del av mina försök att lösa uppgiften (du behöver inte läsa igenom den ville bara bevisat att jag försökt), känns som jag missar något uppenbart.

Här är ett annat alternativ, för den intresserade;

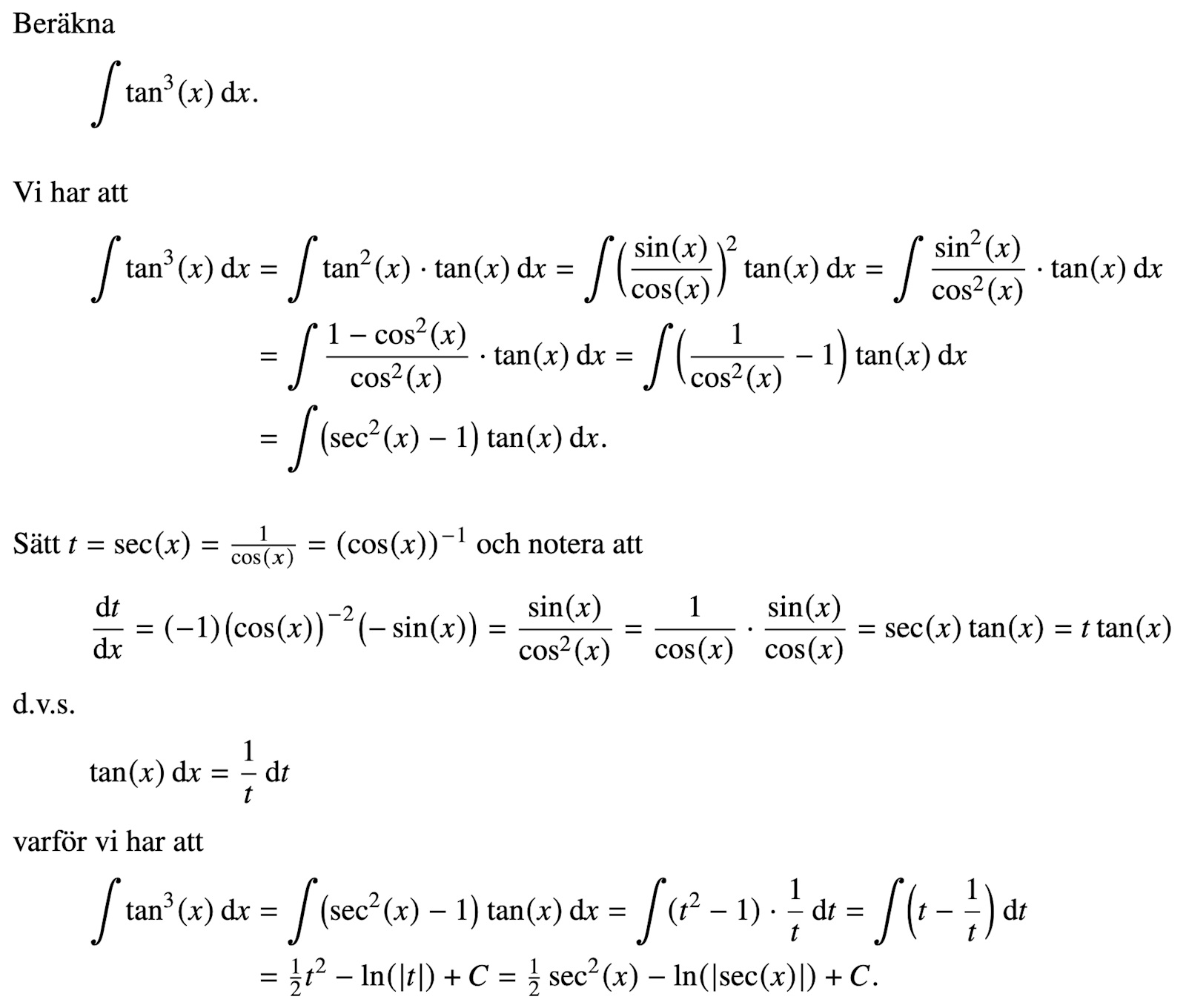
Fast integralen du behöver lösa för diffekvationen blir inte (tanx)³. Det blir (sinx)³/(cosx)⁴.

Du har missat upphöjt i 2 när du multiplicerat den integrerande faktorn. 

En sak som kan vara intressant att notera om den (tydligen felaktiga) integralen är att man faktiskt kan få två svar. Antingen får man svaret som vi fick, eller så kan man få:

$\displaystyle \int_{}^{}\tan^3 x\mathrm{d}x=\int_{}^{}\tan x\left(\sec^2x-1 \right)\mathrm{d}x=\int_{}^{}\tan x\sec^2 x\mathrm{d}x-\int_{}^{}\mathrm{d}x=\frac{\tan^2x}{2}+\ln\left(\cos x \right)+C$

När jag kom att tänka på detta igår blev jag extremt förvirrad. Men det är så att det finns ett samband mellan $\tan^2 x$ och $\sec^2 x$, där skillnaden är en konstant. Detta bakas in i +C:et. :)