interferens, I vilket eller vilka av nedanstående fall ligger P på en nodlinje?
Anordningen AOB (se figuren) svänger med konstant frekvens fram och tillbaka kring en axel genom O vinkelrätt mot papperets plan så att spetsarna A och B växelvis doppar ned i vattnet.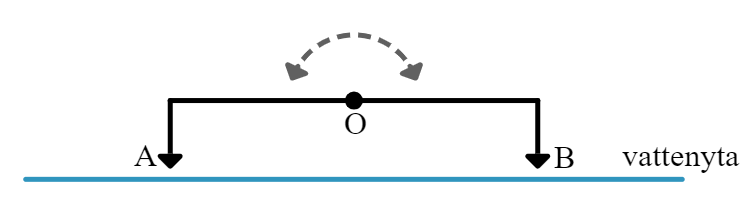
Våglängden på de vågor som utgår från A och B är 4,0 cm. P är en punkt på vattenytan. I vilket eller vilka av nedanstående fall ligger P på en nodlinje? Skillnaden mellan avstånden PA och PB är
Jag fick fram svaren 2 och 6 men det blir inte rätt eftersom dom inte är ifas. Jag förstår inte hur jag ska räkna
Jag blev tvungen att läsa texten flera gånger om för att begripa vad uppgiften ens handlade om. Normalt sett brukar man ha vattenytan i papprets plan så man kan rita upp bilder och tänka.
Det jag tror är nycklarna är att anordningen som förbinder de två spetsarna är en stång och att den har en konstant frekvens. Detta innebär att då den ena spetsen är på sitt djupaste läge är den andra på sitt grundaste läge. Med andra ord, då en topp genereras vid den ena spetsen genereras samtidigt en dal vid den andra spetsen.
Så du vet att de inte är i fas, utan de är i perfekt ofas. Räcker det för att på bilden du visat markera vilka punkter emellan spetsarna som kommer vara nodpunkter? Börja med att bara tänka det som en endimensionell linje.
Bedinsis skrev:Jag blev tvungen att läsa texten flera gånger om för att begripa vad uppgiften ens handlade om. Normalt sett brukar man ha vattenytan i papprets plan så man kan rita upp bilder och tänka.
Det jag tror är nycklarna är att anordningen som förbinder de två spetsarna är en stång och att den har en konstant frekvens. Detta innebär att då den ena spetsen är på sitt djupaste läge är den andra på sitt grundaste läge. Med andra ord, då en topp genereras vid den ena spetsen genereras samtidigt en dal vid den andra spetsen.
Så du vet att de inte är i fas, utan de är i perfekt ofas. Räcker det för att på bilden du visat markera vilka punkter emellan spetsarna som kommer vara nodpunkter? Börja med att bara tänka det som en endimensionell linje.
Jag förstår forfarande inte
Hm. De är inte snälla nog att avslöja avståndet mellan A och B. Det gör det knepigare.
Låtsas om att avståndet mellan A och B är ett specifikt värde. Låt säga 12 cm, eftersom det är jämnt delbart på 4.
Låtsas nu om att vi har en ögonblicksbild där A just nu är i botten, dvs. den genererar en dal. Och den har genererat vågor ett bra tag så att vi kan säga att ytan kryllar av ett vågmönster med våglängder på 4 cm, alla skapade från spets A.
Skissa då upp hur vågorna som skapats från spets A ser ut längs vattenytan; om du vill göra det enkelt för dig kan du bara markera var topparna kommer befinna sig.
Nu hade vi dock två generatorer av vågor, även en från spets B, och denna spets kommer då befinna sig i toppen, dvs. den genererar en topp. Och den har genererat vågor ett bra tag så att vi kan säga att ytan kryllar av ett vågmönster med våglängder på 4 cm, alla skapade från spets B.
Skissa då upp hur vågorna som skapats från spets B ser ut längs vattenytan; om du vill göra det enkelt för dig kan du bara markera var topparna kommer befinna sig.
Om du sedan lägger de två vågmönstren ovanpå varandra, vilka punkter har vi där bidraget från A och B gör så att vågen i själva verket är stilla? Dvs. de två vågmönstren tar ut varandra.
Efter att du gjort det kan du undersöka vad som händer om du ändrar avståndet mellan A och B, och se om du ser något mönster.
Bedinsis skrev:Hm. De är inte snälla nog att avslöja avståndet mellan A och B. Det gör det knepigare.
Låtsas om att avståndet mellan A och B är ett specifikt värde. Låt säga 12 cm, eftersom det är jämnt delbart på 4.
Låtsas nu om att vi har en ögonblicksbild där A just nu är i botten, dvs. den genererar en dal. Och den har genererat vågor ett bra tag så att vi kan säga att ytan kryllar av ett vågmönster med våglängder på 4 cm, alla skapade från spets A.
Skissa då upp hur vågorna som skapats från spets A ser ut längs vattenytan; om du vill göra det enkelt för dig kan du bara markera var topparna kommer befinna sig.
Nu hade vi dock två generatorer av vågor, även en från spets B, och denna spets kommer då befinna sig i toppen, dvs. den genererar en topp. Och den har genererat vågor ett bra tag så att vi kan säga att ytan kryllar av ett vågmönster med våglängder på 4 cm, alla skapade från spets B.
Skissa då upp hur vågorna som skapats från spets B ser ut längs vattenytan; om du vill göra det enkelt för dig kan du bara markera var topparna kommer befinna sig.
Om du sedan lägger de två vågmönstren ovanpå varandra, vilka punkter har vi där bidraget från A och B gör så att vågen i själva verket är stilla? Dvs. de två vågmönstren tar ut varandra.
Efter att du gjort det kan du undersöka vad som händer om du ändrar avståndet mellan A och B, och se om du ser något mönster.
hur kan jag skissa vågorna
Vågorna som utgår från A ritar du genom att rita ett vågmönster där det finns en dal vid spets A och alla andra dalar dyker upp på avstånd om 4 cm.
Vågorna som utgår från B ritar du genom att rita ett vågmönster där det finns en topp vid spets B och alla andra toppar dyker upp på avstånd om 4 cm.
De två vågmönstren kommer vara identiska så när som på en fasförskjutning.
Bedinsis skrev:Vågorna som utgår från A ritar du genom att rita ett vågmönster där det finns en dal vid spets A och alla andra dalar dyker upp på avstånd om 4 cm.
Vågorna som utgår från B ritar du genom att rita ett vågmönster där det finns en topp vid spets B och alla andra toppar dyker upp på avstånd om 4 cm.
De två vågmönstren kommer vara identiska så när som på en fasförskjutning.
såhär?
Försök ladda upp bilden igen, jag får bara en [saknad bild]-symbol.
Bedinsis skrev:Försök ladda upp bilden igen, jag får bara en [saknad bild]-symbol.
bolibompa skrev:Bedinsis skrev:Försök ladda upp bilden igen, jag får bara en [saknad bild]-symbol.
ska jag hitta i vilket avstånd dem hamnar i fas?
Se där, nu funkar det.
Och jag tycker att du har gjort rätt och att jag har valt dumma siffror eftersom att i det här läget så tar varje topp från A ut varje dal från B och vice versa så den här ögonblicksbilden illustrerar att just nu så är vattenytan plan.
Hade A och B varit i fas hade vi dock också fått ögonblicksbilder ibland då de två vågpartierna tar ut varandra. Vad som sedan händer är att om vi låter tiden gå kommer det visa sig att det finns punkter där så är fallet hela tiden medan i andra punkter kommer vi istället få maximal svängning. Så är även fallet här, då de två generatorerna är förskjutna med en halv våglängd.
Tänk efter om tiden går framåt från det här läget. Nöj dig med punkterna mellan A och B.
Då kommer hela vågpaketet som generas av A röra sig en bit till höger och hela vågpaketet som genereras av B röra sig en bit till vänster. Vad kommer den då resulterande vågen att bli? Du kan pröva att ändra hur mycket eller lite du vill för att få fram för att olika mycket av tiden har gått. Hittar du några nodpunkter?
(jag kommer sticka och gymma nu så jag kommer inte kunna svara, så någon annan får gärna ta vid)
Fick du rätt på den?
Det är fritt fram att posta ytterligare frågor annars.
Bedinsis skrev:Fick du rätt på den?
Det är fritt fram att posta ytterligare frågor annars.
Nej, jag förstår fortfarande inte.
Bedinsis skrev:Fick du rätt på den?
Det är fritt fram att posta ytterligare frågor annars.
Kollade facit och det står att det är förskjuten en halv våglängd
Förstår du hur som nodlinjer uppkommer?
