Integrera fram volymen av ett koniskt cirkelsegment

Hej och välkommen till PA!

Jag lite svårt att förstå hur du menar att din kon med ett cirkelsegment som bas skulle se ut. Skulle du kunna skicka en bild?

Hej, tack :)

Här kommer bilden. Observera att det inte är en halvcirkel utan ett cirkelsegment då den inte är skuren mitt genom cirkeln.

Volymberäkningen går ut på att summera bidragen från tunna skivor parallella med basytan.

När det gäller en hel kon är dessa skivor cirkelformade och har därför arean $A=\pi r^2$, där radien $r$ beror på x-koordinaten.

När det gäller din "skurna" kon så kan du göra på exakt samma sätt, men där gäller att skivorna inte är cirkelformade utan istället har formen av cirkelsegment. Det gäller då att hitta en formel för arean av ett sådant cirkelsegment.

Arean för cirkelsegmentet är A=0,5*r²*(v-sinv). Dock vet jag inte hur jag integrerar fram volymen då jag måste kunna representera cirkelsegmentet med koordinater i något plan och kanske fungerar det inte med xy-planet utan att jag kanske måste integrera med en dubbelintegral? Hmm jag vet fortfarande inte.

Rita en bild som visar fallet med den hela konen, där du även lagt in ett koordinatsystem i två dimensioner (så att konen alltså ser ut som en triangel) så tar vi det vidare därifrån.

Här kommer bilden på konen med en cirkel som bas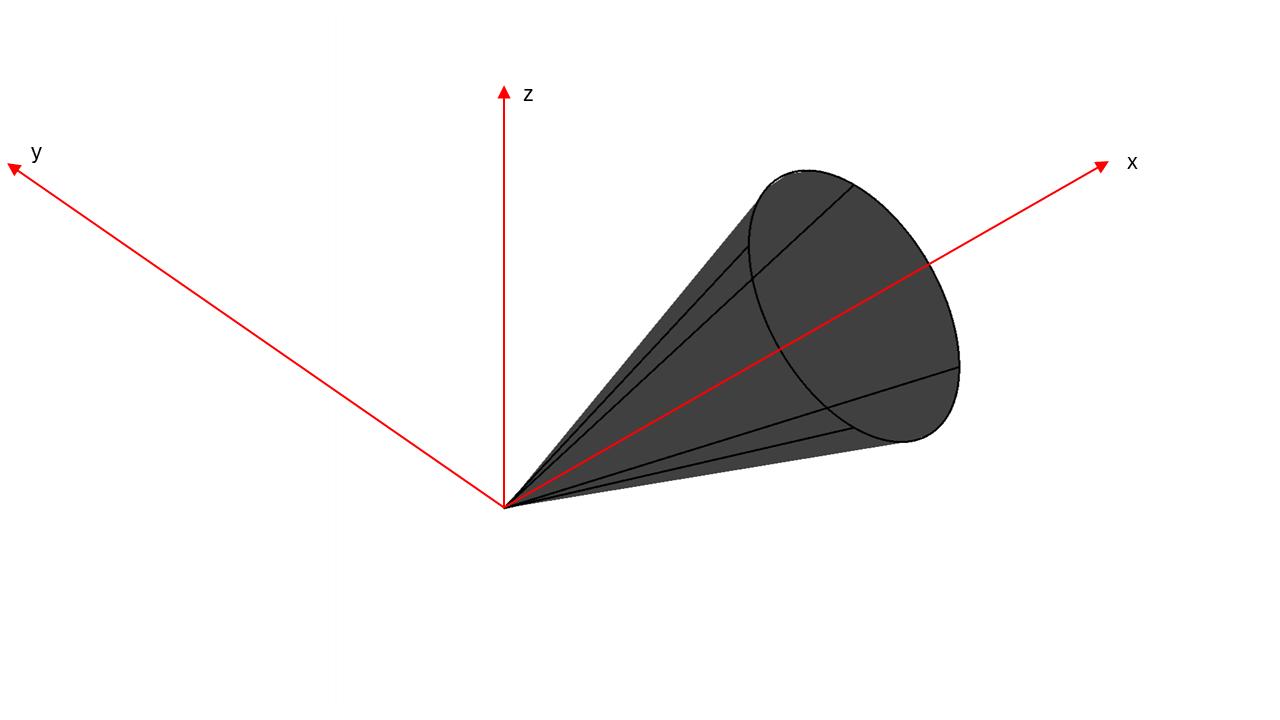

Bra.

Vrid nu bilden så att du endast visar xz-planet.

här är den vriden

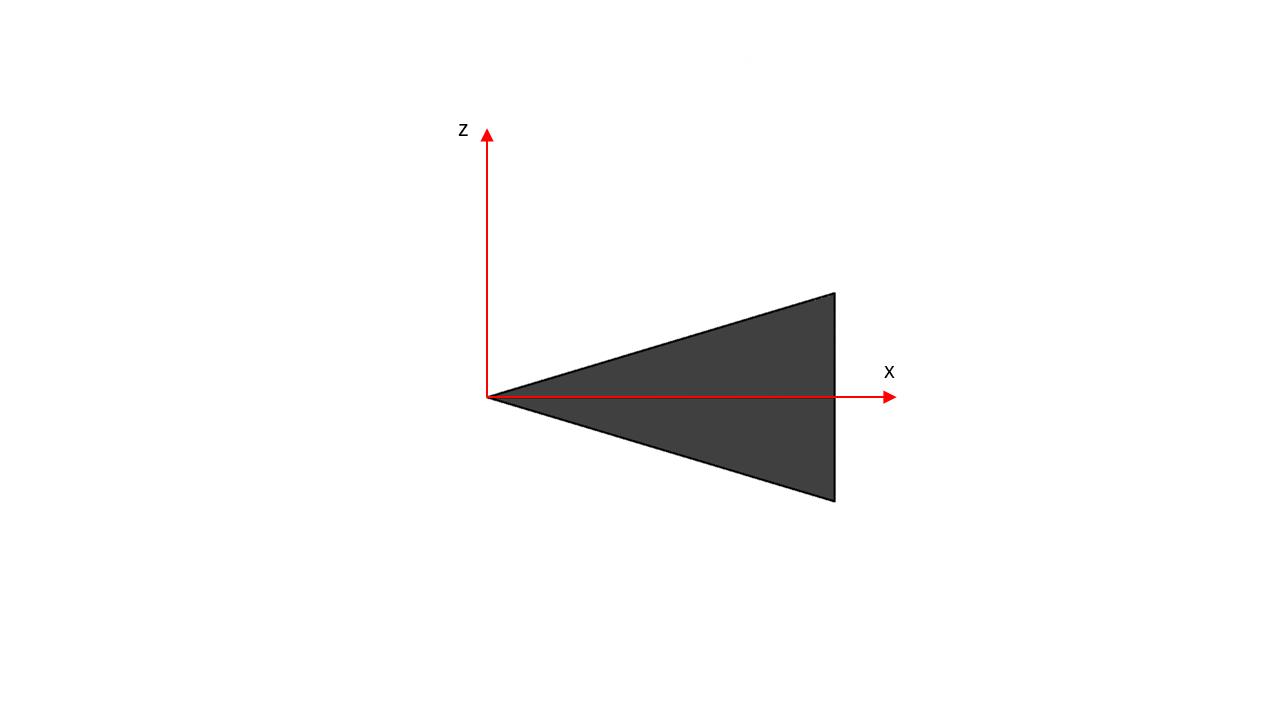
Snyggt.

Här har jag ritat in radien på en cirkulär skiva vid x-koordinaten x. Den har radien r.

Skivans area är då $A=\pi r^2$, där $r$ beror av $x$ enligt ett linjärt samband.

Är du med på att konens volym då kan beräknas genom att man summerar bidragen från dessa skivor?

ja, det är jag med på. men hur relaterar vi konen till cirkelsegmentet?

Volymen av en kon är väl alltid höjden x basarean / 3.

Basens form spelar ingen roll - om jag kommer ihåg rätt.

Nej, volymen är inte alltid höjden x basarean / 3 då det endast gäller för en cirkel som bas. jag har redan kontrollerat volymen för en kon med ett cirkelsegment som bas och när jag räknade enligt Vsegment=Asegment*h/3 så stämmer det inte med det verkliga resultatet. jag har provat att rita upp det här i 3D i ett CAD-program för att kontrollera volymen av konen med ett cirkelsegment som bas och det blev inte samma resultat. jag kan därmed ta reda på vad volymen ska bli för ett specialfall. Vi kan utgå från r=4 m och h=10 m. Då blir Acirkel=50,27 m². Vkon.cirkel=Acirkel*h/3=167,6 m³. om vi har 2 st koner med exakt samma geometri i samma punkt och vi förflyttar den ena konen 2 m i xz-planet så skapas ett överlapp som består av 2 st cirkelsegment vid baserna. volymen för ett sådant cirkelsegment ska bli Vsegment=18,442 m³ enligt den framtagna modellen i CAD-programmet. jag vill alltså härleda en formel som ger mig svaret 18,442 m³ för mitt specialfall :)

jag råkade skriva fel. Parallellförflyningen för mitt specialfall är 4,0 m

Formeln gäller för alla koner. Du måste räknat fel någonstans.

Klurigmatte skrev:

ja, det är jag med på. men hur relaterar vi konen till cirkelsegmentet?

Är du med på att din "skurna" kon ser ut så här från samma perspektiv?

ja det är jag med på Yngve 

Klurigmatte skrev:

[...]

om vi har 2 st koner med exakt samma geometri i samma punkt och vi förflyttar den ena konen 2 m i xz-planet så skapas ett överlapp som består av 2 st cirkelsegment vid baserna. volymen för ett sådant cirkelsegment ska bli Vsegment=18,442 m³ enligt den framtagna modellen i CAD-programmet. jag vill alltså härleda en formel som ger mig svaret 18,442 m³ för mitt specialfall :)

Vänta lite nu.

Förflyttar i vilken riktning? Vilket överlapp? Kan du illustrera?

Det här specialfallet verkar vara något helt annat än den "skurna" kon som du snyggt illustrerade i svar #3 och som åtminstone jag har pratat om sedan dess.

jag vill räkna ut följande volym i första hand men är ändå intresserad av den volymen som du illustrerade. vi kanske kan börja med fallet från svar #3 och sedan gå vidare med nedan.

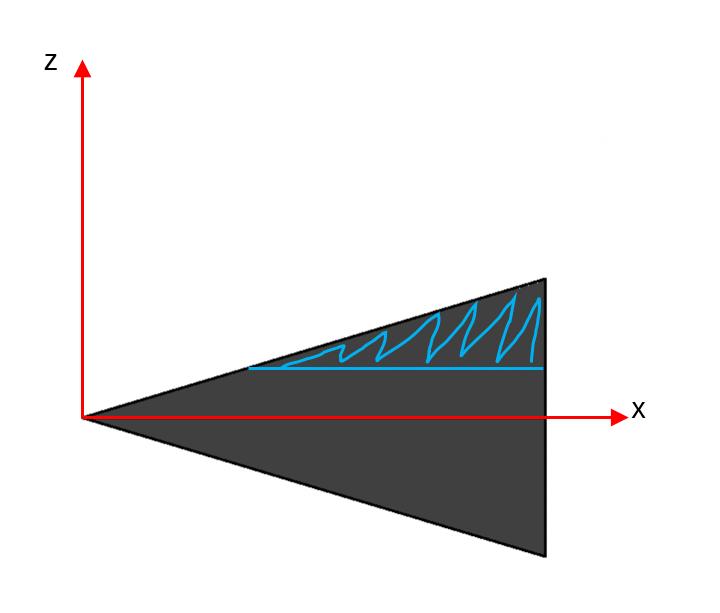
OK då är det något helt annat än det jag trodde och min bild i svar #16 stämmer då inte alls.

Om du vill använda en formel för att beräkna volymen av specialfallet så kan du använda V = B*h/3, precis som PATENTERAMERA skrev.

Om du istället vill integrera så kan du göra det, baserat på följande bild.

Jag vet inte riktigt om jag vet hur du menar men menar du att B=r2-r1 ? Då blir B=r-2=4-2=2. h=x2-x1=10-5=5. V=B*h/3=2*5/3=3,33 m3, vilket inte stämmer med min CAD-modell där V_CAD.modell=18,442 m³. Hela konens volym från början är ju V=pi*r²*h/3=pi*4²*10/3=167,55 m³. vad har blivit tokigt?

Volymen för nedanstående del ska bli V=18,442 m³. Vilken formel ger detta värde?

Klurigmatte skrev:

Volymen för nedanstående del ska bli V=18,442 m³. Vilken formel ger detta värde?

Jag får volymen till $V=\frac{40}{3}(\frac{2\pi}{3}-\frac{\sqrt{3}}{2})\approx16,38$ m³.

Baserat på formeln $V=\frac{B\cdot h}{3}$, där höjden $h=5$ m och basaean $B=0,5r^2(v-\sin(v))$, där basradien $r=4$ m och vinkeln $v=\frac{2\pi}{3}$ radianer.

Antingen har jag räknat fel eller så räknar vi ändå på olika saker.