Integrera (1+2z+3^z2)/(3z^3) med gränserna 1 och 2
Hej jag behöver hjälp med att lösa denna integral. Jag repeterar inför att börja universitet och jag har helt glömt hur man ska göra i sånna här situationer. Ja försöker kolla på formelbladet med det blir ändå inte rätt vad gör ja för fel eller vart ska ja börja? Mitt andra försök är från när jag använde Photomath men jag har aldrig behövt göra så att ja delar upp integralen vad ja kan minnas iallafall så ja vet ändå inte vad ja ska göra…

Att dela upp integralen är ett bra första steg. Då kan du förenkla varje uttryck för sig. Ex. . Och på liknande sätt för tredje termen.
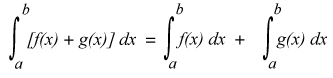
Okej tack! Då kan ja fortsätta på det då men de som gjorde att ja inte fortsatte var att de kändes fel och jag vet inte vad den primitiva funktionen är till 1/(z^3) eller (3z^2)/(z^3)…
Om funktionen f(x) = xn så är den primitiva funktionen F(x) = xn+1/(n+1) + C. Detta gäller även för negativa värden på n (men inte för n = -1).
Smaragdalena skrev:Om funktionen f(x) = xn så är den primitiva funktionen F(x) = xn+1/(n+1) + C. Detta gäller även för negativa värden på n (men inte för n = -1).
Blir f(z)= 1/(z^3) till F(z)=z/(z^4)/4 då?
Nej, om du verkligen menar att f(x) = 1/z3 och z3 är en konstant, så är den primitiva funktionen F(x) = x/z3 + C.
Om du menar f(x) = 1/x3 = x-3 så blir F(x) = -x-2/2 + C.
Smaragdalena skrev:Nej, om du verkligen menar att f(x) = 1/z3 och z3 är en konstant, så är den primitiva funktionen F(x) = x/z3 + C.
Om du menar f(x) = 1/x3 = x-3 så blir F(x) = -x-2/2 + C.
Oj ja jag menade det andra jag råkade skriva x istället för z… förlåt, jag har ändrat det nu!:) okej tack. Ja förstår det då som att du skriver om 1/x3 till x-3. jag förstå hur den primitiva funktionen blir -x-2/2+c då men ja undrar varför man inte gör något med 1an? I detta fall blir det ju bara gånger 1 så den försvinner men om det hade varit 2/x3 istället blir den primitiva funktionen då -2x-2/2 +c ? Varför gäller inte regeln att f(x)=k => F(x)=kx +c nu i täljaren? Är det för att man alltid ska skriva om bråket som en multiplikation med en negativ potens istället?
Mollyhej skrev:Oj ja jag menade det andra jag råkade skriva x istället för z… förlåt, jag har ändrat det nu!:) okej tack. Ja förstår det då som att du skriver om 1/x3 till x-3. jag förstå hur den primitiva funktionen blir -x-2/2+c då men ja undrar varför man inte gör något med 1an? I detta fall blir det ju bara gånger 1 så den försvinner men om det hade varit 2/x3 istället blir den primitiva funktionen då -2x-2/2 +c ?
Om du har funktionen f(x) = kxn så är den primitiva funktionen F(x) = kxn+1/(n+1).
Varför gäller inte regeln att f(x)=k => F(x)=kx +c nu i täljaren? Är det för att man alltid ska skriva om bråket som en multiplikation med en negativ potens istället?
Var får du en etta i täljaren? Menar du i termen ? När du deriverar funktioner av typen f(x) = xn får du aldrig någon derivata som har exponenten -1, så det måste vara någon annan funktion som har derivatan x-1. Det visar sig att det är logaritmfunktionen som har denna egenskap.



