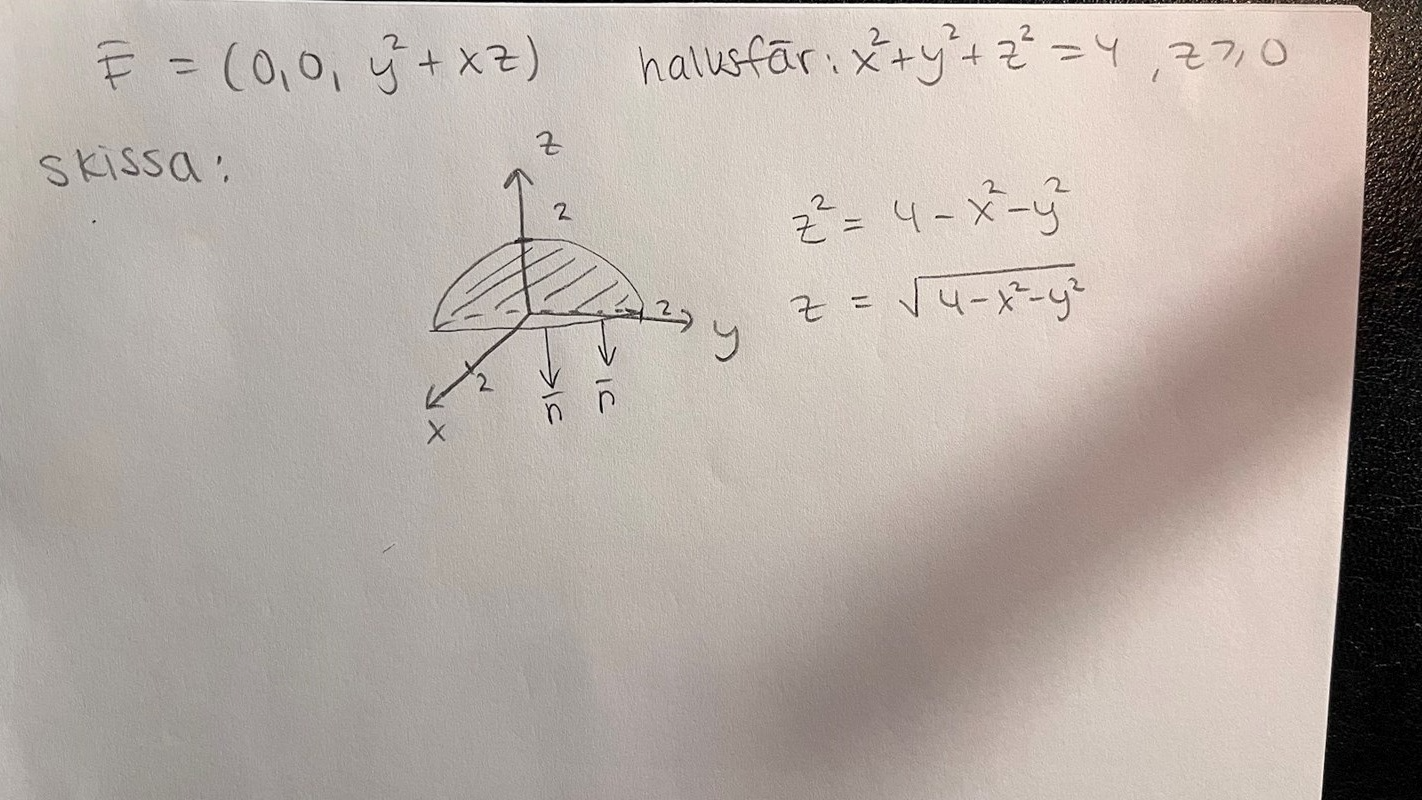Integrationsgränser för z

Har jag rätt om att säga att z varierar från sqrt3 till 4-r^2 ? (då x^2 + y^2 = 1)
.Nej, det stämmer inte. x2+y2 = 1 beskriver en cirkel med radie 1 i x/y-planet.
På den cirkeln är z = överallt (eftersom x2 +y2 +z2 = 4 där blir till 1+z2 = 4 och z 0).
Hur menar du? Blir inte z^2 = 3 då och därmed z= sqrt3?
flippainte skrev:Hur menar du? Blir inte z^2 = 3 då och därmed z= sqrt3?
Jo, jag skrev fel först. Har rättat nu.
Men z är konstant på den cirkeln.
Vad menas med konstant? På den tidigare frågan jag gjorde så beskrevs z= 2-sqrt(x^2+y^2) och vi fick att x^2+y^2 ≤ 1 och tog x^2+y^2 = 1 i z för att få en av gränserna z=1. Är det inte samma typ av metod nu?
Men hur får du in x2 + y2 = 1 i detta problem?
Det står att du har en halvsfär. Rita in denna i ett koordinatsystem.
Enligt min skiss ska z gå från 0 till 2
Eller är det z= sqrt(4-x^2-y^2) till 2 då 0 inte är explicit inkluderad?
flippainte skrev:Enligt min skiss ska z gå från 0 till 2
Lägg upp din skiss här!
Precis. Har du tänkt på om du skall använda Gauss eller om du skall integrera flödet genom sfären direkt?
Tänkte ta Gauss men har ett problem. Har svårt med att hitta nedre gränsen för z då jag antar (enligt skiss) att övre ska vara 2 ?
Dessutom vet jag inte hur man integrerar flödet direkt? Man måste ju betrakta den nedre buktiga delen oxå
Du kan använda cylinderkoordinater. r går från 0 till 2. z går från 0 till . Vinkeln går från 0 till . Verkar det rimligt?
Kan man använda sfäriska koordinater: r går från 0 till 2, phi går från 0 till pi/2 och theta går från 0 till 2pi?
Ja, det ser ut att gå bra.

När jag försökte lösa denna (liknande) så använde jag cylindriska koordinater istället för sfäriska. Jag fick rätt på buktiga delen men fel på den övre där de fick 2pi/5 fick jag -4pi/15.
Går det att använda cylindriska här ens?
Tog gränserna z går från 0 till sqrt(1-r^2), r går från 0 till 1 och theta går från 0 till 2pi. Och Integralen var r^2.
I cylinderkoordinater blir integranden r2 + z2. Och dV = rdrdzd.
Är inte z=0 i integranden?
Nej, du skall ju utvärdera en volymsintegral över hela halvklotet, så z är inte 0 överallt. Det måste med.
Däremot när du utvärderar flödet genom ”botten” på klotet så är z = 0.
Tack!