Integralkalkyl fundamentalsats

Jag tycker att Wikipedias bevis med hjälp av medelvärdessatsen för integraler är ganska enkelt att begripa. Du måste dock känna till medelvärdessatsen för integraler, men den är inte så krånglig alls!

Okej 🙂

Får ta reda på vad det är först. 

Nej, jag begriper inte. Får köpa att det fungerar för att det gör det bara för tillfället.

Vad är det du tycker är svårt? Vi kan säkerligen reda ut det här, om du har lust. Vad är det för bevis av medelvärdessatsen som du har stött på? Vissa är krångligare än andra.

Jo. Gärna.

Jag förstår medelvärdessatsen, tror jag. Tänker att det den säger mer eller mindre känns som en självklarhet på något sätt. Men varför det skulle vara intressant i det här fallet förstår jag inte.

Okej. Vi börjar med att formulera medelvärdessatsen för integraler då:

Sats 1 (medelvärdessatsen för integraler):

Om $f$ är en kontinuerlig funktion på $[a,b]$ så finns det ett $\xi \in [a,b]$, sådant att:

$\displaystyle \int_{a}^{b}f=f\left(\xi\right)\left(b-a\right)$

Utifrån detta är vi nu redo att bevisa att analysens fundamentalsats, alltså:

$\displaystyle \int_{a}^{b}f=F\left(b\right)-F\left(a\right)$

Bevis:

Definiera $\displaystyle F\left(x\right):=\int_{a}^{x}f\left(t\right)\mathrm{d}t$, där $f$ är en kontinuerlig funktion.

Enligt derivatans definition har vi då att:

$\displaystyle F'\left(x\right)=\lim_{h \to 0} \frac{F\left(x+h\right)-F\left(x\right)}{h}=\lim_{h\to0}\frac{1}{h}\left[\int_{a}^{x+h}f\left(t\right)\mathrm{d}t-\int_{a}^{x}f\left(t\right)\mathrm{d}t\right]$

$\displaystyle =\lim_{h \to 0} \frac{1}{h}\int_{x}^{x+h}f\left(t\right)\mathrm{d}t$

Enligt medelvärdessatsen för integraler existerar det något $\xi \in [x,x+h]$ sådant att:

$\displaystyle \displaystyle \lim_{h \to 0} \int_{x}^{x+h}f\left(t\right)\mathrm{d}t =\lim_{h \to 0} \frac{1}{h}f\left(\xi\right)\left(x+h-x\right)=\lim_{h \to 0} \frac{1}{h}f\left(\xi\right)h=\lim_{h \to 0} f\left(\xi\right)$

Då $h \to 0$ kommer $\xi \to x$. Därför har vi att:

$\displaystyle \lim_{h \to 0} f\left(\xi\right)=f\left(x\right)$

Detta innebär att $F$ är en primitiv funktion till $f$ på $[a,b]$. Vi vet att klassen av alla primitiva funktioner till en funktion kan fångas genom tillägg av en konstantterm. Således har vi att:

$G\left(x\right) = F\left(x\right)+C$

$C$ bestäms enkelt genom insättning av $x=a$ i sambandet ovan. Detta ger $C=G(a)$, eller med andra ord $F\left(x\right) = G\left(x\right)-G\left(a\right)$, eller med andra ord:

$\displaystyle \int_{a}^{b}f=F\left(b\right)=G\left(b\right)-G\left(a\right)$

där $G$ är någon primitiv till $f$.

Tillägg: 10 nov 2024 23:41

Som du ser kan vi göra det väldigt enkelt för oss med hjälp av medelvärdessatsen.

Detta är inte ett bevis, men snarare en liten "intuitiv" anledning till satsen som jag gillar:
Tänk dig att vi har någon funktion, $f(x)$ och en annan okänd funktion, $A(x)$. Det $A(x)$ ger tillbaka är arean mellan $f(x)$ och x-axeln från 0 (spelar ingen roll, i detta fall väljer vi från för argumentets och enkelhetens skull) upp till $x$. 
Exempelvis skulle funktionen kunna se ut såhär och $A(5)$ skulle ge denna area under kurvan

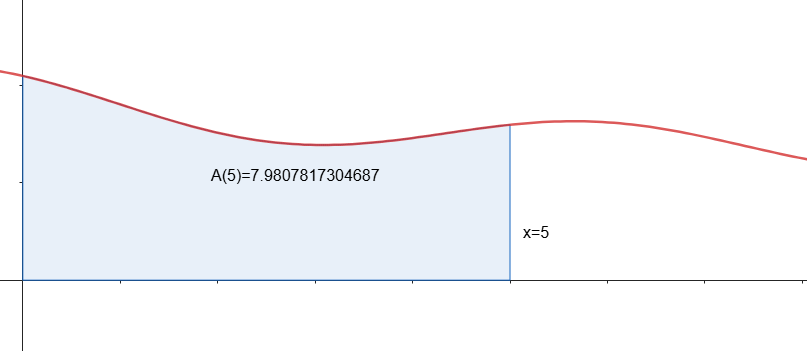Då har vi att vid någon punkt $x=b$ är arean under $f(x)$ lika med $A(b)$. 
Tänk nu att vi vill hitta arean mellan någon annan punkt lite längre bort från $b$. Denna punkt är distansen $h$ bort och har alltså x-värdet $x=b+h$. Eftersom $A(b+h)$ ger arean från 0 till $b+h$ och $A(b)$ ger arean från 0 till b så kommer $A(b+h)-A(b)$ ge arean från 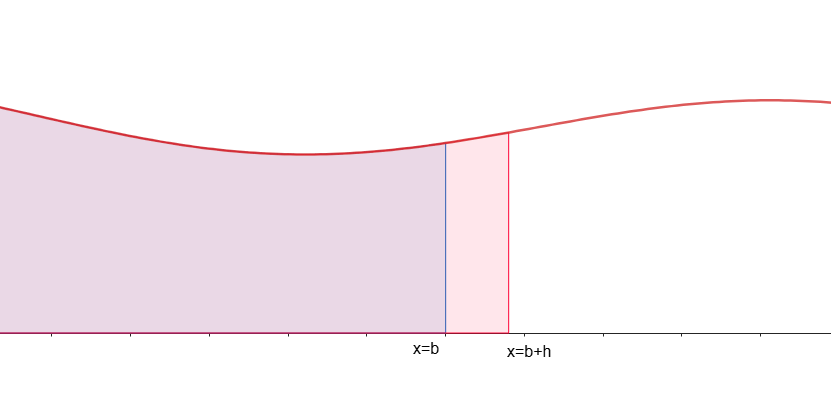$b$ till $b+h$.
Samtidigt kan vi få ett ungefärligt värde på arean mellan $b$ och $b+h$ genom att använda en rektangel. Distansen mellan $b$ och $b+h$ är så klart $h$. Samtidigt är höjden $f(b)$

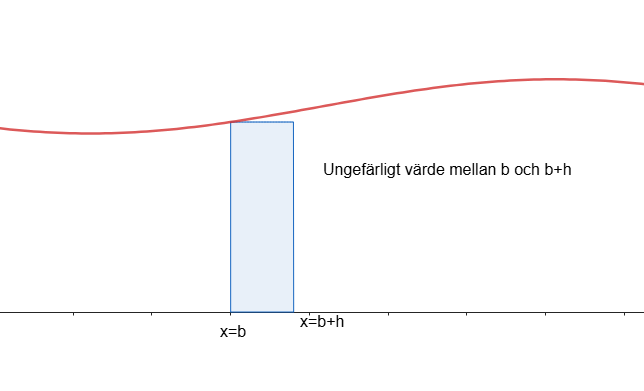Rektangeln area kan vi beräkna som basen gånger höjden eller då $h \cdot f(b)$.
Eftersom dessa två areor är ungefär samma får vi att $h \cdot f(b) \approx A(b+h) - A(b)$
Delar vi med $h$ får vi $f(b)$ $\displaystyle\approx  \frac{A(b+h) - A(b)}{h}$. Detta ser ju ut som derivatans definition! Sedan kan man ta gränsvärdet när $h$ går mot noll för att exakt få derivatans definition i högerledet
$f(b)$ "=" $\displaystyle \lim_{h\to 0}{\frac{A(b+h) - A(b)}{h}}$ $= A'(b)$
Slutligen får vi att $f(b)$ "=" $A'(b)$, vilket vi kan formulera om som att antiderivatan till $f(x)$ ger arean under kurvan. 

Vill nämna igen att detta verkligen inte är ett bevis av integralkalkylens fundamentalsats. Jag minns bara att min matte 3 lärare visade detta på tavlan som en liten intuitiv anledning / redovisning varför satsen fungerar.

AlexMus intuitiva förklaring går att visa rigoröst i ramverk som icke-standardanalys. I själva verket finns det många satser som man kan bevisa intuitivt för sig själv på exakt det sättet som AlexMu föreslår. T.ex. formeln för längden på en kurva kan man motivera på exakt samma sätt.

naytte skrev:

AlexMus intuitiva förklaring går att visa rigoröst i ramverk som icke-standardanalys. I själva verket finns det många satser som man kan bevisa intuitivt för sig själv på exakt det sättet som AlexMu föreslår. T.ex. formeln för längden på en kurva kan man motivera på exakt samma sätt.

Intressant! Har inte sett några sådana bevis men kommer kolla på det imorgon

naytte skrev:

---

Tillägg: 10 nov 2024 23:41

Som du ser kan vi göra det väldigt enkelt för oss med hjälp av medelvärdessatsen.

Well..

Tack för ditt svar, men vad betyder ${\int }_a^b f= f\left(\epsilon \right) (b-a)$ till att börja med..

Det där tecknet är så kallat epsilon vad jag läser mig till, som betyder.. vadå, punkten i en kurva där lutningen är densamma som en sekant dragen ifrån start till slutpunkt på x axeln? Nej, det betyder ingenting utan är bara en variabel. Summan från a till b i en funktion f är lika med.. nej, jag vet inte hur jag ska tolka det.

AlexMu skrev:

Detta är inte ett bevis, men snarare en liten "intuitiv" anledning till satsen som jag gillar:
Tänk dig att vi har någon funktion, $f(x)$ och en annan okänd funktion, $A(x)$. Det $A(x)$ ger tillbaka är arean mellan $f(x)$ och x-axeln från 0 (spelar ingen roll, i detta fall väljer vi från för argumentets och enkelhetens skull) upp till $x$. 
Exempelvis skulle funktionen kunna se ut såhär och $A(5)$ skulle ge denna area under kurvan

Då har vi att vid någon punkt $x=b$ är arean under $f(x)$ lika med $A(b)$. 
Tänk nu att vi vill hitta arean mellan någon annan punkt lite längre bort från $b$. Denna punkt är distansen $h$ bort och har alltså x-värdet $x=b+h$. Eftersom $A(b+h)$ ger arean från 0 till $b+h$ och $A(b)$ ger arean från 0 till b så kommer $A(b+h)-A(b)$ ge arean från $b$ till $b+h$.
Samtidigt kan vi få ett ungefärligt värde på arean mellan $b$ och $b+h$ genom att använda en rektangel. Distansen mellan $b$ och $b+h$ är så klart $h$. Samtidigt är höjden $f(b)$

Rektangeln area kan vi beräkna som basen gånger höjden eller då $h \cdot f(b)$.
Eftersom dessa två areor är ungefär samma får vi att $h \cdot f(b) \approx A(b+h) - A(b)$
Delar vi med $h$ får vi $f(b)$ $\displaystyle\approx  \frac{A(b+h) - A(b)}{h}$. Detta ser ju ut som derivatans definition! Sedan kan man ta gränsvärdet när $h$ går mot noll för att exakt få derivatans definition i högerledet
$f(b)$ "=" $\displaystyle \lim_{h\to 0}{\frac{A(b+h) - A(b)}{h}}$ $= A'(b)$
Slutligen får vi att $f(b)$ "=" $A'(b)$, vilket vi kan formulera om som att antiderivatan till $f(x)$ ger arean under kurvan. 

Vill nämna igen att detta verkligen inte är ett bevis av integralkalkylens fundamentalsats. Jag minns bara att min matte 3 lärare visade detta på tavlan som en liten intuitiv anledning / redovisning varför satsen fungerar.

Behöver inget bevis.. :) jag vill bara mentalt kunna acceptera det som sant och förstå vad jag egentligen gör när jag beräknar någonting, liksom. Tecknet epsilon naytte använde är väl typ för att representera din idé här med rektangeln fast visa att båda går mot varandra och slutligen är samma sak om man använder sig av ett infinitesimalt avstånd mellan, eller någonting sådant.

Och tack, förresten.

Dkcre skrev:

naytte skrev:

---

Tillägg: 10 nov 2024 23:41

Som du ser kan vi göra det väldigt enkelt för oss med hjälp av medelvärdessatsen.

Well..

Tack för ditt svar, men vad betyder ${\int }_a^b f= f\left(\epsilon \right) (b-a)$ till att börja med..

Det där tecknet är så kallat epsilon vad jag läser mig till, som betyder.. vadå, punkten i en kurva där lutningen är densamma som en sekant dragen ifrån start till slutpunkt på x axeln? Nej, det betyder ingenting utan är bara en variabel. Summan från a till b i en funktion f är lika med.. nej, jag vet inte hur jag ska tolka det.

Det betyder inget speciellt egentligen, det är bara något tal mellan b och a som gör att likheten är sann. Det är exakt det här som medelvärdessatsen säger, att ett sådant tal finns för alla kontinuerliga funktioner. Tecknet är för övrigt den grekiska bokstaven xi.

Kan det vara så att du har läst på om medelvärdessatsen och inte medelvärdessatsen för integraler? De är två olika satser. (eller de är egentligen samma sats skrivna på olika sätt, men om man vill använda den för att bevisa analysens fundamentalsats måste man bevisa den lite annorlunda för integraler).

naytte skrev:

Dkcre skrev:

Visa föregående citat

naytte skrev:

---

Tillägg: 10 nov 2024 23:41

Som du ser kan vi göra det väldigt enkelt för oss med hjälp av medelvärdessatsen.

Well..

Tack för ditt svar, men vad betyder ${\int }_a^b f= f\left(\epsilon \right) (b-a)$ till att börja med..

Det där tecknet är så kallat epsilon vad jag läser mig till, som betyder.. vadå, punkten i en kurva där lutningen är densamma som en sekant dragen ifrån start till slutpunkt på x axeln? Nej, det betyder ingenting utan är bara en variabel. Summan från a till b i en funktion f är lika med.. nej, jag vet inte hur jag ska tolka det.

Det betyder inget speciellt egentligen, det är bara något tal mellan b och a som gör att likheten är sann. Det är exakt det här som medelvärdessatsen säger, att ett sådant tal finns för alla kontinuerliga funktioner. Tecknet är för övrigt den grekiska bokstaven xi.

---

Kan det vara så att du har läst på om medelvärdessatsen och inte medelvärdessatsen för integraler? De är två olika satser. (eller de är egentligen samma sats skrivna på olika sätt, men om man vill använda den för att bevisa analysens fundamentalsats måste man bevisa den lite annorlunda för integraler)...

Ja, det stämmer ju. Okej, har inte sett tecknet förut.

Läste om den nu och det betyder att det finns en punkt i intervallet där summan mellan a och b, eller integralen är lika med värdet för en punkt c multiplicerat med avståndet mellan a och b, uh, tror jag. Och då är den här punkten av någon anledning också medelvärdet av funktionen..

Det kommer ta mig flera veckor att förstå det här så tror jag gör bäst i att fortsätta räkna och ha en liten idé om vad jag gör och vara nöjd med det för tillfället. Annars kommer jag inte komma någonstans.

Tack för hjälpen.