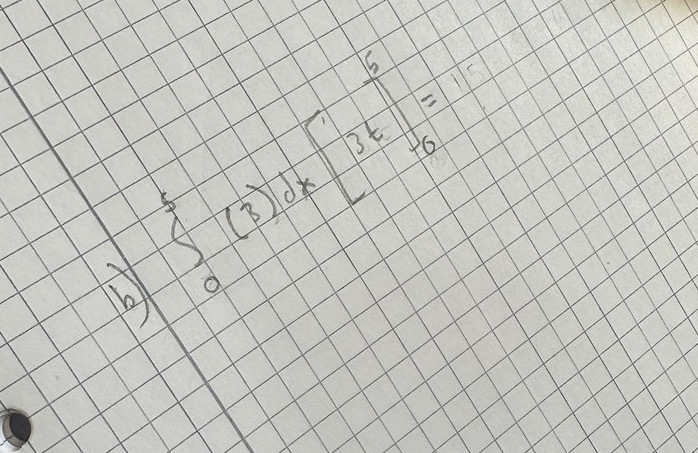Integraler
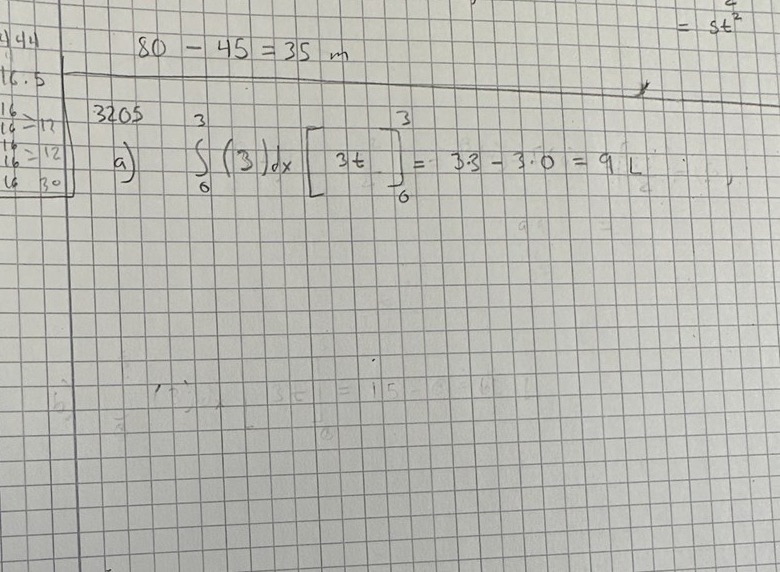
 hejsan skulle jag kunna få hjälp på a)
hejsan skulle jag kunna få hjälp på a)
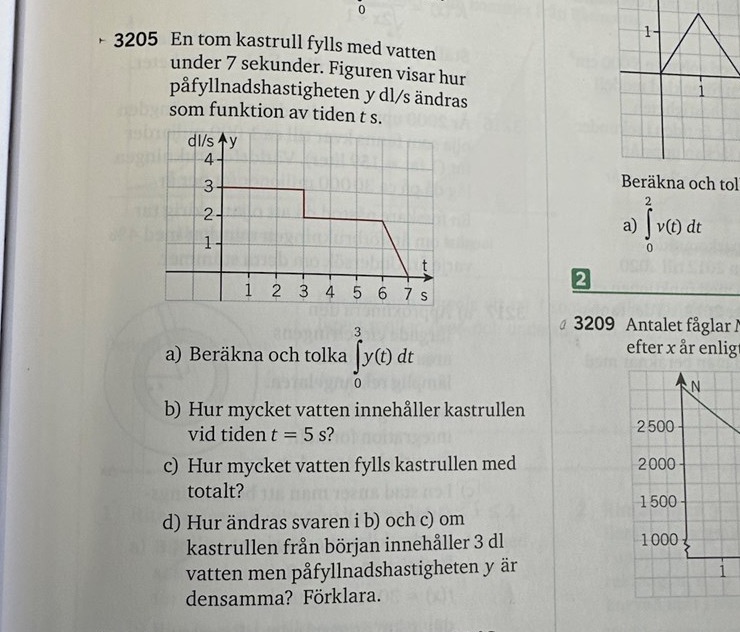
Det som kan hjälpa med tolkning är att kolla på enheterna. I detta fall är y-axeln dl/s och x-axeln är tid, s. Integralen har enheten som är produkten av y-axelns och x-axelns enheter (eftersom integralen är area). Vilken enhet skulle detta vara?
Ett annat sätt att tänka är att y kan ses som en derivata. Derivatan till något är påfyllnadshastighet. Vad skulle då antiderivatan beskriva för något?
Antiderivatan skulle bara visa hur mycket vatten har som har fyllts på i kastrullen efter en viss tid (t)
på b) ska man:
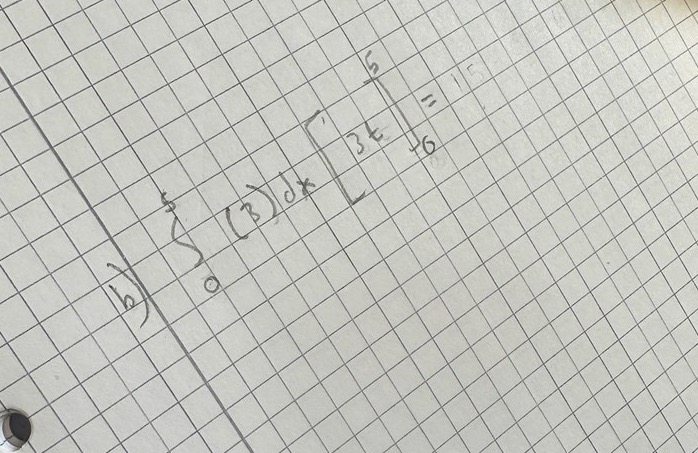
Du måste ta hänsyn till att påfyllnadshastigheten varierar under tidens gång.
Biorr skrev:Antiderivatan skulle bara visa hur mycket vatten har som har fyllts på i kastrullen efter en viss tid (t)
på b) ska man:
Geometriskt är integralen arean under kurvan. Vi ser i figuren att y inte alltid är 3, detta måste du ta hänsyn till när du räknar.
Det går till y=2 och sedan till y= 1?
typ: 3t+2t +1t
Ja, först är y = 3, sen y = 2 men mellan t = 6 och t = 7 sker en konstant minskning av hastigheten. Eftersom integranden (funktionen man integrerar) skiljer sig så behöver man ställa upp två integraler och summera dem.
 Gör det att göra c såhär?
Gör det att göra c såhär?
 hur gör man d)?
hur gör man d)?
Biorr skrev:Gör det att göra c såhär?
Ditt svar är rätt (9+6+1 = 16), men den sista integralen är fel. Den ska vara ∫76(14-2x)d.
Är du med på varför?
Kommentar: Men jagctror att tanken är att du ska räkma rutor, inte beräkna integraler.
hur gör man d)?
Det du räknar ut i b och c är hur mycket vatten som fylls på. Kan det ringa någon klocka hos dig?
Jag är inte med på varför 14-2x på sista integralen på c)
Biorr skrev:Jag är inte med på varför 14-2x på sista integralen på c)
Det är så funktionen ser ut i det intervallet.