Integraler

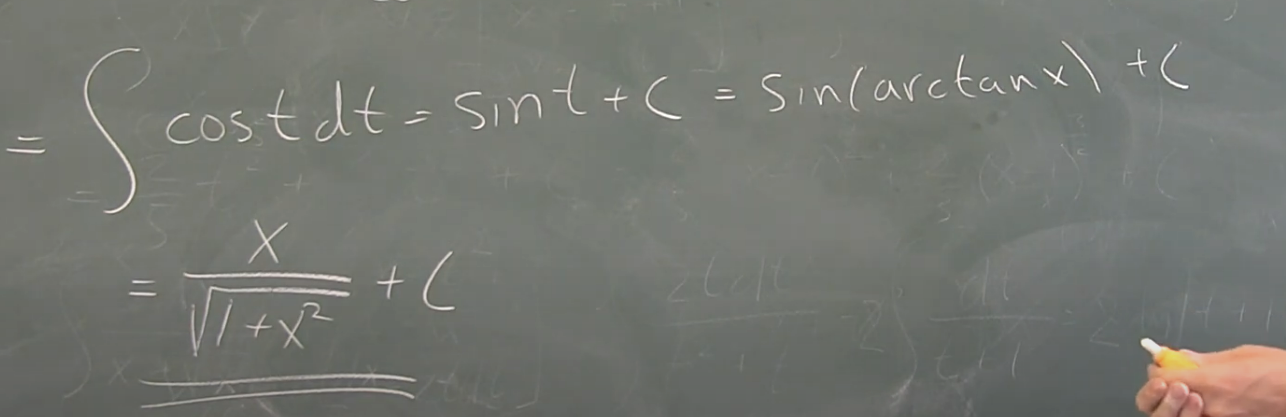
Hej, jag förstod inte sista steget hur kunde kan gå från $\sin(\arctan(x)$ till $\frac{x}{\sqrt{1+x^2}}$ ?

Har formlerna för derivering av arcus funktioner, påminner om dem. ser inte hur det man bli det.

Tack för svar!

Om du tänker på en rätvinklig triangel:

$a r c \tan (x) = α \Rightarrow x = \tan (α) \Rightarrow x = \frac{a}{b} \Rightarrow a = b x$

$\sin (a r c \tan (x)) = \sin (α) = \frac{a}{c} = \frac{a}{\sqrt{a^{2} + b^{2}}} = \frac{b x}{\sqrt{b^{2} x^{2} + b^{2}}} = \frac{x}{\sqrt{x^{2} + 1}}$

Macilaci skrev:
Om du tänker på en rätvinklig triangel:

$a r c \tan (x) = α \Rightarrow x = \tan (α) \Rightarrow x = \frac{a}{b} \Rightarrow a = b x$

$\sin (a r c \tan (x)) = \sin (α) = \frac{a}{c} = \frac{a}{\sqrt{a^{2} + b^{2}}} = \frac{b x}{\sqrt{b^{2} x^{2} + b^{2}}} = \frac{x}{\sqrt{x^{2} + 1}}$

tusen tack! Nu förstår jag

Svara