Integral / primitiv funktion

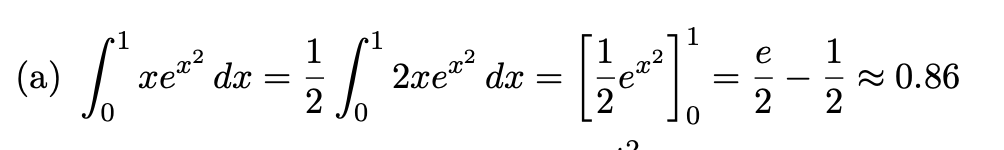
Översta är frågan och under är lösningsförslaget. Jag förstår inte helt hur man har gjort, men kanske att man kanske kan använda partiellintegration (?). Jag är dock osäker och har glömt hur man får en primitiv funktion till ex2? Är det ex22x?
Avokado12345 skrev:
Översta är frågan och under är lösningsförslaget. Jag förstår inte helt hur man har gjort, men kanske att man kanske kan använda partiellintegration (?). Jag är dock osäker och har glömt hur man får en primitiv funktion till ex2? Är det ex22x?
Okej vänta de har förlängt med 2/2, brytit ut 1/2 ur integralen, och så verkar ex22xvara en primitiv funktion, och så förkortas 2x bort, och sen multiplicera med 1/2 och sen beräkna integralen tror jag?
Det dem har gjort är nog substitution. u=x^2.
observera att: u=x2=>du=2xdx<=>dx=12xdu. Därför är det smidigt att förlänga med 2. Integraler blir därför:
12∫2xeu×12xdu=12∫eudu=12ex2
pepsi1968 skrev:Det dem har gjort är nog substitution. u=x^2.
observera att: u=x2=>du=2xdx<=>dx=12xdu. Därför är det smidigt att förlänga med 2. Integraler blir därför:
12∫2xeu×12xdu=12∫eudu=12ex2
Okej, jag förstår. Tack så mycket!
din funktion xex^2 är av typen
f'(x)*ef(x) dvs du har en sammansatt funktion med den inre derivatan framför
Om man vet hur ex deriveras kanske man inser att e(x^2) har derivatan 2xe(x^2)
och kan då hitta en primitiv till integranden
Jag tror att dem har tänkt på att:
ddx[ex2]
Eftersom din integrand bara saknar en tvåa för att bli detta
har dem lagt till en tvåa i integranden och en halva utanför.
Att sedan integrera derivatan av ett uttryck är ganska lätt.






