Integral och derivata

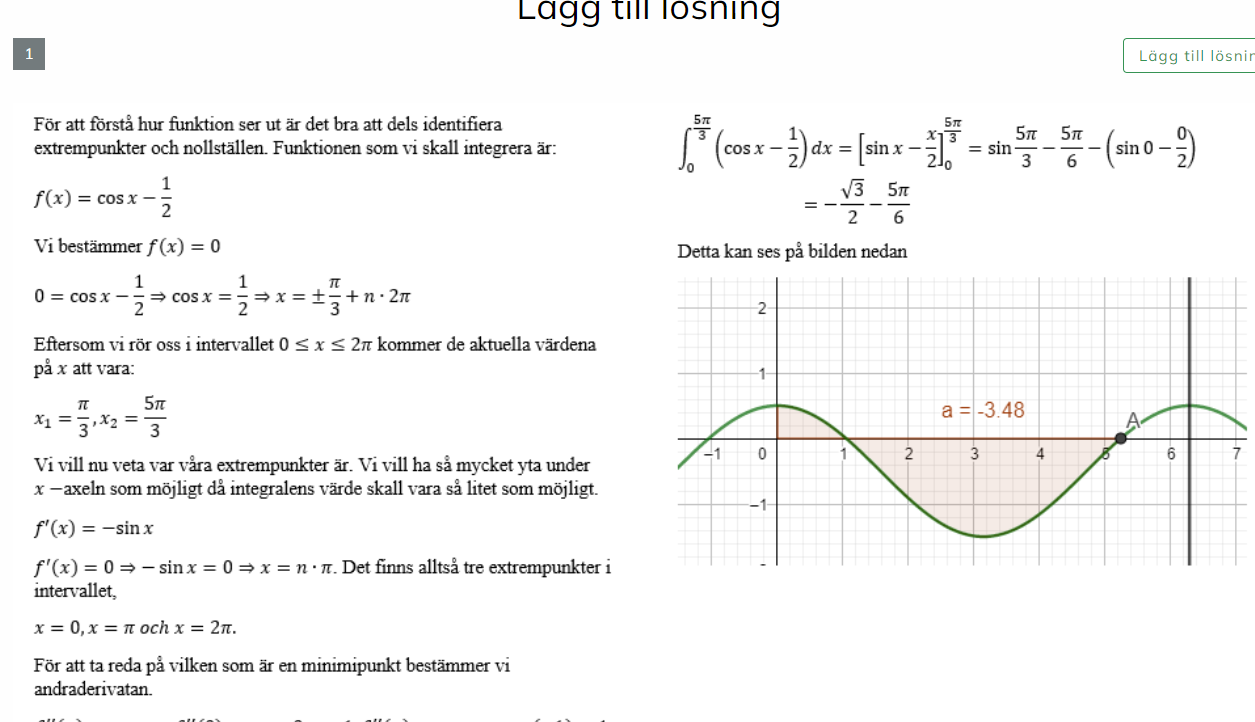
Ang den här uppgiften. Varför är det inte exakt avståndet pi mellan nollställena dvs x= pi/3 och 5pi/3. Borde man inte få fram det andra nollstället genom att ta pi/3+3pi/3?! Men då får man 4pi/3. Vad gör jag för fel?

$f (x) = \cos x - \frac{1}{2}$ och det är detta -1/2 som gör det.

Om du förflyttar funktionen ännu längre nedåt, t.ex. $f (x) = \cos x - 1$

så får du $0 + n \cdot 2 π$ för nollställen.

Splash.e skrev:
Varför är det inte exakt avståndet pi mellan nollställena?

Cosinusfunktionen har en period på 2pi, inte pi.

Avståndet mellan två närliggande nollställen som "hänger ihop" är därför 2pi.

Alla nollställen där grafen är på väg uppåt "hänger ihop".
Alla nollställen där grafen är på väg neråt "hänger ihop".

Avståndet mellan två närliggande nollställen som inte hänger ihop kan vara vad som helst mellan 0 och 2pi.

Detta avstånd beror på värdet a i uttrycket cos(x)-a, precis som Macilaci förklarade.

Svara