Integral med Lim
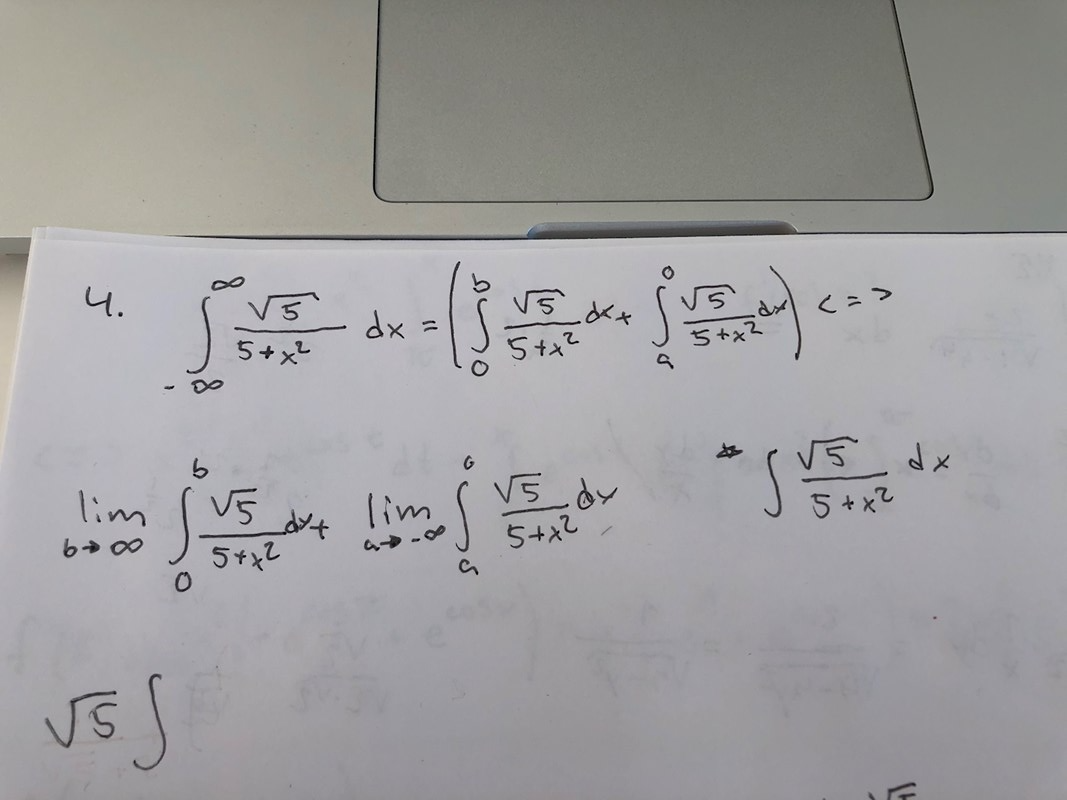 Hur får man fram att substitution är x/roten ur 5?
Hur får man fram att substitution är x/roten ur 5?
När jag ser någonting på formen (k och m är konstanter) tänker jag alltid på arctangens, eftersom arctangens har derivatan . Om vi kan få vårt uttryck att ha den formen, kan vi integrera till arctangens. I detta fall är det femman som är i vägen. Vi skulle vilja substituera bort x till något så att vi kan bryta ut och få bort femman.
Om vi provar att bryta ut en femma nu, får vi nämnaren . Vi sätter därför variabeln t till , och får då integranden . Hur blir det med differentialen (det som i vår ursprungsintegral var "dx")? :)
dx=
Alltså ser integralen ut så här:
Stort tack för hjälpen.
Japp! Glöm bara inte att byta tillbaka till x när du har integrerat. Och glöm inte +C! :D
Jag roterade din bild så det är enklare att läsa. Notera att du själv kan rotera felroterade bilder genom att trycka på redigera -> trycka på bilden -> använda pilarna för att rotera bilden. /Dracaena, moderator
Smutstvätt skrev:Japp! Glöm bara inte att byta tillbaka till x när du har integrerat. Och glöm inte +C! :D
Nejdå, glömmer aldrig C ;).
Dracaena skrev:Jag roterade din bild så det är enklare att läsa. Notera att du själv kan rotera felroterade bilder genom att trycka på redigera -> trycka på bilden -> använda pilarna för att rotera bilden. /Dracaena, moderator
Japp, tack för info.
sebone skrev:Smutstvätt skrev:Japp! Glöm bara inte att byta tillbaka till x när du har integrerat. Och glöm inte +C! :D
Nejdå, glömmer aldrig C ;).

Smutstvätt skrev:sebone skrev:Smutstvätt skrev:Japp! Glöm bara inte att byta tillbaka till x när du har integrerat. Och glöm inte +C! :D
Nejdå, glömmer aldrig C ;).
Hahaha, tur att vi bara glömmer C i matematiken. :D



