Integral med cosinus
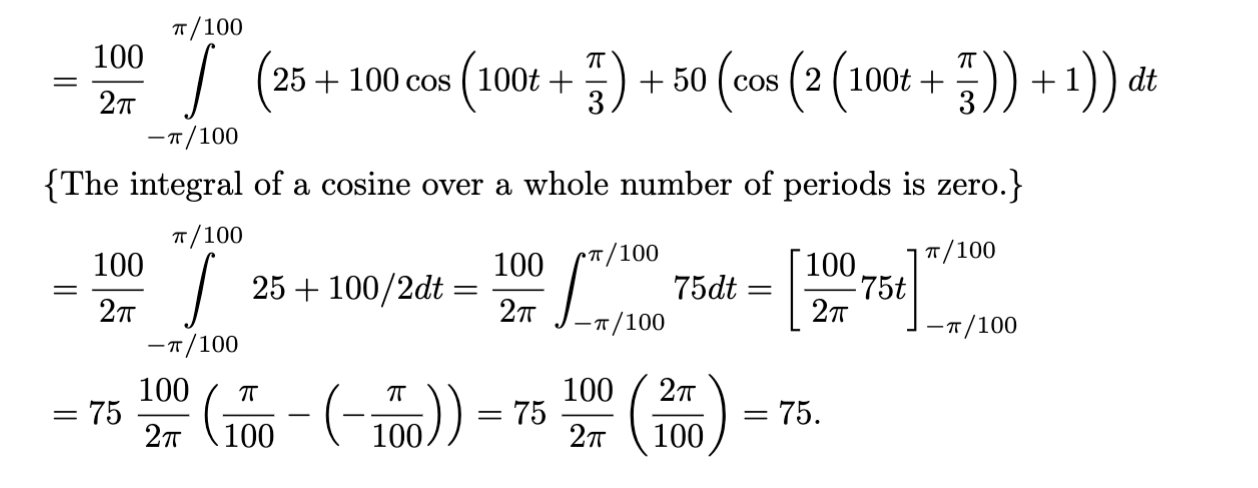
Alltså jag är förvirrad över vad som sker efter den första raden... Periodtiden för den första cosinusfunktionen är /100 så som dom skriver så kommer alltså den delen av integralen att vara noll? sen är det den andra delen kvar, eller? Men jag är osäker på hur man räknar ut den... Jag har glömt en del känner jag... :(
Om du integrerar funktionen cos(x + a) över en hel period, exempelvis mellan x = 0 och x = 2π, så kommer svaret bli 0. Areorna ovan och under x-axeln tar ut varandra. Detsamma gäller förstås om vi t.ex. integrerar från x = 0 till x = 200π. Mer generellt så erhåller vi alltid 0 om vi integrerar över ett helt antal perioder. I uppgiften integrerar vi visserligen från -π/100 till π/100 Men ser du vad som händer med funktionen cos(100t +...) för de integrationsgränserna?
Periodtiden av första cosfunktionen är 2pi/100. Andra cosfunktionen har halva periodtiden, alltså innefattas den också av facits argument varför den blir noll.
Om man läser lite slarvigt i parenteserna kan man missa att
Andra halvan av integranden har en offset:
50* ( cos(v) + 1 )
Okej, men så båda cosinusfunktionerna blir noll (det spelar ingen roll att ena är multiplicerad med 2?) och sen blir det ju 50*1 men de har skrivit det som 100/2 av någon anledning? Så det är därför det blir 25+(100/2) som blir kvar?
Så det är därför det blir 25+(100/2) som blir kvar?
Ja. (Jag tycker också det känns onaturligt att uttryck "det som blir kvar" för 100/2 istället för 50)



