Integral/Bestämning av f(x)dx
Hej,
Uppgiften handlar om att man ska bestämma f(x) dx i en integral från -2 till 6 som går genom punkterna (-2,0), (3,3) och (6,5). Behöver ju inte rita graf på denna.
Hur får man ut vad f(x) dx är, ska man kika på y-värdena?
Mvh/H
Henrik 2 skrev:Hej,
Uppgiften handlar om att man ska bestämma f(x) dx i en integral från -2 till 6 som går genom punkterna (-2,0), (3,3) och (6,5). Behöver ju inte rita graf på denna.
Hur får man ut vad f(x) dx är, ska man kika på y-värdena?
Mvh/H
Jo, det behövs en graf för att åtminstone jag skulle kunna förstå den här uppgiften. Jag skulle lätt kunna rita 10 olika f(x) som alla går genom punkterna (-2,0), (3,3) och (6,5) men är oika däremellan, och som allihop ger olika area mellan funktionen och x-axeln.
Det är väldigt svårt att lösa uppgiften om man har inte grafen med sig. Som Smaragdalena nämnde, så kan man rita många funktioner som passerar igenom dessa tre punkter, fast har olika areor. Kanske finns det mer information som vi kan få utifrån problemet?
Ok, denna är grudläggande nivå men kunde den inte.
Ok, trodde inte en graf behövdes men försöker rita hur den går,hur jag kommer ihåg den. Trodde bara man kunde kika på talet,uppgiften för att få ut den, den e som sagt på grundläggande nivå.
Lägger in den i nästa meddelande.tråd.. Här kommer den så som jag kommer ihåg den, men då jag har anget koordinaterna/punkterna (-2,0), (3,3) och (6,5) så blev jag osäker och skrev 1 o 11 hur den går. Sedan då e integralen från -2 till 6 (som även framgår av x-värden i ändpunkterna)
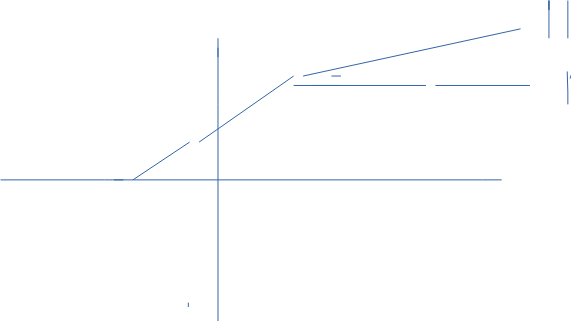
Om du har en bild som här till den här uppgiften: Lägg in den i den här tråden. Det blir så rörigt med flera trådar om samma uppgift.
Se inlägg 4 den ligger där nu, se om man kan få ut något av det.
Man kan gissa att det ska vara räta linjer mellan punkterna, men det är fortfarande en gissning. I så fall kan du använda det du vet om rektanglar och trianglar.
Hur då?
Du förstod att den antingen går som i 1 eller som den som i 11 dvs från -,2,0?
Mvh/H
Jag vet inte vad du frågar, men den slutar i alla fall i (6, 5).
Om uppgiften gäller att beräkna och skissen visar grafen till så kan du räkna fram svaret genom att summera areorna av område A och område B.
Eller genom att integrera en funktion från x = -2 till x = 3 och en annan funktion från x = 3 till x = 6.
Vilka dessa funktioner i så fall är får du klura ut själv.
Det är bra träning att räkna på båda sätten. Om resultaten blir samma så är det troligtvis rätt.

Aha, e det så man gör o delar upp den, då ska vi se. Återkommer o ser om jag kommer fram till ett svar.
Mvh/H
Ok, får fram A till 7,5 men B (som e b*h=a) hur gör man om höjden stiger från 3 till 5, ska man ta genomsnittet,dvs 4, eller det högsta av dem dvs 5?
Mvh/H
Henrik 2 skrev:Ok, får fram A till 7,5
Det stämmer
men B (som e b*h=a) hur gör man om höjden stiger från 3 till 5, ska man ta genomsnittet,dvs 4, eller det högsta av dem dvs 5?
Område B är ett parallelltrapets. Det finns en färdig formel för areaberäkning av en sådan. Det är bra att träna på att använda den formeln.
Ok, har sett en sådan, så parallelltrapets en form av rektangel (eller?), kikar formelbladet.
a=h(a+b)/2
h=3? a=3 (från 3 till 6)? b=2 (iom stiger från 3 till 5)? om så
3(3+2)/2
7,5?
A=7,5 B=7,5 o totalt 15 ?
Hur blir detta en funktion,dvs f(x)dx?
Har du skrivit symbolen för delta vid y o med bokstaven D vid x?
Henrik 2 skrev:Har du skrivit symbolen för delta vid y o med bokstaven D vid x?
Nej det är pilar på koordinataxlarna.
Andra alternativet. Nej om man ska integrera vet o förstår jag inte vilka funktionerna e som inte e utsatta?
Ok, så det e pilar.
Henrik 2 skrev:[...]
a=h(a+b)/2
h=3? a=3 (från 3 till 6)? b=2 (iom stiger från 3 till 5)? om så
3(3+2)/2
7,5?
A=7,5 B=7,5 o totalt 15 ?
h är avståndet mellan de två parallella sidorna. I det här fallet så är h = 3.
a och b är längderna av de parallella sidorna, i det här fallet 3 och 5.
Så vi får A = h*(a+b)/2 = 3*(3+5)/2 = 3*4 = 12
Hur blir detta en funktion,dvs f(x)dx?
Det enklaste är.art dela upp grafen i de två intervallen [-2, 3] och [3, 6].
I vart och ett av dessa intervall så är grafen en rät linje.
Vi kan kalla den vänstra delen f(x) och den högra delen g(x).
Försök nu att hitta en linjär funktion f(x) vars graf stämmer med grafen i den vänstra delen [-3, 3] och en annan linjär funktion g(x).vars graf stämmer med grafen i den högra delen [3, 6].
Ok, så allt korrekt men inte 2 utan man tar 5 som e det högsta y-värdet. Det blir då 12, o då e det 7,5 (A)plus 12(B)=19,5 som säger vad?
Ok, två intervall, -2,3 och 3,6 o grafen e i dessa båda är en rät linje.
Vänstra kan kallas f(x) ochden högra g(x).
Du menade -2,3 va o inte -3,3?
Nej, vet inte hur man hittar en linjär funktion, förstår inte än i vart fall.
Henrik 2 skrev:Ok, så allt korrekt men inte 2 utan man tar 5 som e det högsta y-värdet. Det blir då 12, o då e det 7,5 (A)plus 12(B)=19,5 som säger vad?
Det säger att arean under grafen ör 19,5 ae.
Ok, två intervall, -2,3 och 3,6 o grafen e i dessa båda är en rät linje.
Vänstra kan kallas f(x) ochden högra g(x).
Du menade -2,3 va o inte -3,3?
Ja, jag skrev fel
Nej, vet inte hur man hittar en linjär funktion, förstår inte än i vart fall.
Läs detta avsnitt och fråga oss sedan om allt du vill att vi förklarar närmare.
Där står det hur man utgår från två punkter på en linje och med hjälp av dem.kan bestämma linjens k-värde (dvs lutningen) och m-värde (dvs var linjen skär y-axeln).
Just det arean under denna graf e 19,5. Men vet inte hur man får ut en funktion av det, men kikar länk.
k=delta y/delta x=y2 -y1/x2 -x1
Är det så man ska göra här, men om så vilka koordinater ska väljas,förvirrad?
Vad görs med arean på 19,5 a.e reltarerat till f(x)dx som ska hittaS?
Mvh/H
Henrik 2 skrev:k=delta y/delta x=y2 -y1/x2 -x1
Är det så man ska göra här, men om så vilka koordinater ska väljas,förvirrad?
Det är två olika linjer, så du behöver ta fram två olika funktioner. Min bild i svar #10 visar vilka koordinater som gäller för de båda linjerna.
Vad görs med arean på 19,5 a.e reltarerat till f(x)dx som ska hittaS?
Det tar vi sen. Börja med att bestämma f(x) och g(x) enligt ovan.
Ok, så jag ska ta fram två olika funktioner först. Nej,förstår inte, ser koordinaterna men förstår inte ska jag ta först -2,0 som då blir x1 o y1 o 3,3 som blir x2 o y2 o sedan i nästa intervall så blir 3,3 x1 o y1 o 6,5 x2 o y2?
Nej, förstår inte.
Mvh/H
Henrik 2 skrev:Ok, så jag ska ta fram två olika funktioner först. Nej,förstår inte, ser koordinaterna men förstår inte ska jag ta först -2,0 som då blir x1 o y1 o 3,3 som blir x2 o y2 o sedan i nästa intervall så blir 3,3 x1 o y1 o 6,5 x2 o y2?
Ja, det stämmer.
En linje i taget. Den första linjen gpr genom (-2, 0) och (3, 3). Det betyder att den första linjens k-värde blir k1 = (3-0)/(3-(-2)) = 3/5.
Nu vet du att den första linjens ekvation är y = (3/5)x+m1, där m1 är y-värdet för linjens skärning med y-axeln.
Vi kan bestämma detta y-värde med hjälp av någon av de kända punkterna.
Vi väljer punkten (-2, 0), vilket ger oss att 0 = (3/5)*(-2)+m1, dvs m1 = 6/5.
Den första linjens ekvation är alltså y = (3/5)x+6/5.
Motsvarande funktion kan skrivas f(x) =;(3/5)x+6/5.
========
Gör nu på samma sätt med den andra linjen för att bestämma g(x).
Tips: Här är de två punkterna (3, 3) och (6, 5)
Ska gå nu, men tänkte jag rätt då med detta så en linje i taget o nu gav du mig all info, men jag tänkte rätt med det jag skrev då?
Mvh/H
Henrik 2 skrev:Ska gå nu, men tänkte jag rätt då med detta så en linje i taget o nu gav du mig all info, men jag tänkte rätt med det jag skrev då?
Mvh/H
Jag gav dig bara all info om den ena linjen, så att du skulle kunna härma min metod ord för ord, rad för rad när du själv tar fram ekvationen och funktionen för den andra linjen. Byt då endast ut siffrorna.
Det du skrev i svar #25 stämmer.
Yes, förstår o testar den andra linjen Men blir inte det -1,2, dvs -6/5 då du gånger med -2?
Så ena funktionen blir y=(3/5)x-6/5
Blir den andra g(x)=(2/3)x+1?
Om så vad görs nu med dessa två funktioner och 19,5 a.e?
Det här var enbart på E-nivå, detta känns så mycket mer komplicerat än så. Är detta verkligen sättet man löser denna för det känns som C-A nivå på denna?
Mvh/H
Henrik 2 skrev:Yes, förstår o testar den andra linjen Men blir inte det -1,2, dvs -6/5 då du gånger med -2?
Så ena funktionen blir y=(3/5)x-6/5
Räkna själv vidare och lös ut m1 ur sambandet 0 = (3/5)*(-2)+m1
Visa alla dina räknesteg.
Får du att m1 är lila med -6/5 då?
Blir den andra g(x)=(2/3)x+1?
Ja, det stämmer. Bra att du skriver parenteser runt k-värdet.
Om så vad görs nu med dessa två funktioner och 19,5 a.e?
Du kan integrera f(x) från x = -2 till x = 3 och g(x) från x = 3 till x = 6.
Det här var enbart på E-nivå, detta känns så mycket mer komplicerat än så. Är detta verkligen sättet man löser denna för det känns som C-A nivå på denna?
Det beror på hur frågan är formulerad.
Nu gissade vi ju bara hur uppgiften löd och vad den gick ut på.
Dessutom uppmanade jag dig att lösa den påhittade uppgiften på två olika sätt, för att träna och förhoppningsvis både se samband mellan area/integral och se att det ofta går att lösa uppgifter på olika sätt.
Frågan var formulerad mer eller mindre på detta sätt.
Jus det man flyttar över -1,2 till HL således blir det 1,2 eller 6/5?
Ska jag integrera dessa funktioner med de olika x:n,jaha superlång lösning för en E-uppgift..:)
Men vart kommer 19,5 a.e in som vi beräknat?
E lite ,än så länge ,lost i denna fråga/svar. Men super att vi går igenom detta då jag inte visste att man skulle lösa den så här om man inte får f(x) direkt.
Henrik 2 skrev:[...]
Jus det man flyttar över -1,2 till HL således blir det 1,2 eller 6/5?
Just det
Ska jag integrera dessa funktioner med de olika x:n,jaha superlång lösning för en E-uppgift..:)
Se svae #10, vi visste inte hur uppgiften var formulerad så gissade på det, vi visste inte att det var en E-uppgift.
Därför föreslog jag två olika lösningar och uppmanade jag dig att pröva båda för att träna.
Om du hade givit oss mer information om uppgiften från början så hade vi kunnat peka på lösningsmetoden för E-nivå direkt, nämligen den som använde areaberäkning av triangel och parallelltrapets.
Då hade vi inte blandar in vare sig f(x), g(x) eller integraler.
Men vart kommer 19,5 a.e in som vi beräknat?
Se svar #21
Hej,
Men hur ska den lösas på E-nivå då med det som vi gort av triangel och paralleltrapets, vad blir lösning då med dessa 19,5 a.e då vi ska ha ut en funktion av det f(x)dx?
Mvh/H
Henrik 2 skrev:Men hur ska den lösas på E-nivå då med det som vi gort av triangel och paralleltrapets, vad blir lösning då med dessa 19,5 a.e då vi ska ha ut en funktion av det f(x)dx?
Mvh/H
Det går inte att säga hur en fråga vars lydelse vi inte känner till ska lösas på E-nivå.
Om antagandet i början av svar #10 är rätt så är en lämplig lösningsmetod på E-nivå att summera arean av triangeln och parallelltrapetset.
Detta fungerar eftersom detta värde är lika med integralens värde.
Ok, men hur lyder funktionen f(x) dx av 19,5 ae?
är inte en funktion utan istället en del av ett integraluttryck, som t.ex. i .
Här kallas
- integraltecken
- undre gräns
- övre gräns
- integrand
- differential.
Integranden är en funktion
=========
Uppgiften gäller antagligen att bestämma , där är den (styckvis) linjära funktion som går genom de givna punkterna.
Då är svaret 19,5 a.e.
≈=========
Om frågan istället (eller dessutom).hade varit att bestämma den (styckvis linjära),funktion som går genom de givna punkterna så är svaret att
- då
- då
Det är alltså helt OK att beskriva en funktion med olika.uttryck i olika intervall.
Hej,
Hm, jag vet ju inte men f(x) att det kan skrivas so 19,5 a.e . Jag e mer van att f(x)dx skrivs som när du tar i de olika intervallen 3/5x+6/5 då x är lika med eller större än -2 men mindre eller lika stor som 3 och 2/3x+1 då x är större eller lika med 3 eller mindre eller lika stor som 6.
Om man ska skapa en primitiv funktion hur ska man göra det av 19,5 a.e,det går ju inte?
Mvh/H
P.s vet inte vad man ska svara i denna fråga. 19,5 a.e o beräkna areorna i paralleltrapets och i triangeln o lägga ihop dem eller med räta linjen då man får ut funktionen,lutning och m som man kan göra en primitiv funktion av?
När du ser frågan spontant, vill man ha ut av svaret 19,5 a.e. i o m kordinaterna som dem anger o det går ut på att man ska ha kunskap om att göra två olika områden o tillämpa formler för rektangelns och parallelltrapetsens areor?
Ska det vara x mindre än 3 o mindre än 6 eller glömde du lika med?
Henrik 2 skrev:Ska det vara x mindre än 3 o mindre än 6 eller glömde du lika med?
Jag skrev fel, det ska vara .
Ok, bara en liten not,då jag såg det o lade märkte till det.
Henrik 2 skrev:Hm, jag vet ju inte men f(x) att det kan skrivas so 19,5 a.e .
Nej, f(x) är en funktion och 19,5 a.e. är ett värde. Det är inte samma sak.
Jag e mer van att f(x)dx skrivs som när du tar i de olika intervallen 3/5x+6/5 då x är lika med eller större än -2 men mindre eller lika stor som 3 och 2/3x+1 då x är större eller lika med 3 eller mindre eller lika stor som 6.
Jag förstår inte alls vad du menar här. Vad menar du när du skriver "f(x) dx"?
Och vad menar du när du skriver "tar i de olika intervallen"?
Om man ska skapa en primitiv funktion hur ska man göra det av 19,5 a.e,det går ju inte?
Om du vill svara på E-nivå så ska du inte besvara frågan med hjälp av integraler.
P.s vet inte vad man ska svara i denna fråga. 19,5 a.e o beräkna areorna i paralleltrapets och i triangeln o lägga ihop dem
På E-nivå: Ja.
eller med räta linjen då man får ut funktionen,lutning och m som man kan göra en primitiv funktion av?
På E-nivå: Nej
När du ser frågan spontant, vill man ha ut av svaret 19,5 a.e. i o m kordinaterna som dem anger o det går ut på att man ska ha kunskap om att göra två olika omreden o tillämpa formler för rektangelns och parallelltrapetsens areor?
Jag ser ingen fråga, vi har hittat på den under tiden.
Den fråga vi har hittat på leder spontant till metoden att beräkna områdets area med hjälp av geometri.
Hm, aja. Jag vet inte alls om dem vill att man ska få ut f(x) dx av dessa koordinater som du nu fått av den räta linjen, eller om det då som jag sade e på E-nivå och således bara tillämpa formlerna för triangel och paralleltrapetsen lägga ihop dessa areor. Men verkar som du menar att 19,5 ae e det som man vill ha ut, spontant av dessa koordinater,dvs ett värde o inte f(x)dx.
Henrik 2 skrev:[...]Men verkar som du menar att 19,5 ae e det som man vill ha ut, spontant av dessa koordinater,dvs ett värde o inte f(x)dx.
Återigen, "f(x) dx" är inte ett väldefinierat uttryck, det är en del av en beskrivning av en integral.
Hm, oavsett kommunikationsproblem i frågan o vad man ska ha ut så om du ser frågan o hur man lägger upp den med dessa koordinater och räta linjer är det att dem vill att man ska tillämpa formlerna för arean och se att man delar upp områdena i två delar o lägger ihop dessa?
Aja, du har redan svarat att för E-nivå så e det så.
Mvh/H
Ja. Är det något annat du undrar över?
Nej, nu e denna fråga löst både med ae och med f(x) dx o g(x)dx
Mvh/H
Vad bra. Men skriv inte vare sig "f(x) dx" eller "g(x) dx" utan att förklara vad du egentligen menar.
Ja du vad menar jag egentligen..:)
Men nu e denna uppgift löst oavsett.
Mvh/H




