Integral av ellips
Jag har fastat på detta problem:
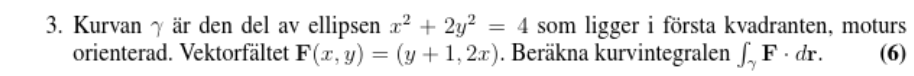
Min initiala tanke var att använda Greens formel, men fick inte riktigt ihop det. Sedan försökte jag bara parametrisera över ellipsen och beräkna integraler över den men tyckte även att det blev komplicerat.
När du använder Greens så är det bra att känna till att arean av en ellips ges av , där a och b är halvaxlarna.
Annars är Greens ganska enkelt. Visa hur långt du kommer.
Jag kom fram till att vilket ger dubbelintegral av areaelementet, därför så räknade jag arean till att bli
Fast tänk på att vi bara tittar på den del som är i första kvadranten, en fjärdedel av hela ellipsen.
Sedan måste du dra bort integralerna längs I och II (se figur).

Tillägg: 30 maj 2024 19:57
Tänk på att Greens bara gäller för sluten kurva.
Juste, men det jag har svårt för är varför i och ii måste bort.
Eftersom kurvan gamma inte är sluten (obs det är linjeintegralen längs gamma som efterfrågas) så kan inte Green tillämpas direkt. Greens funkar dock på den slutna kurvan gamma + I + II, men inte på gamma ensamt.
= .
Så om du bara vill ha integralen längs gamma så får du dra bort linjeintegralerna längs I och II från dubbelintegralen.
Klart som korvspad?
Jaa! Tack så mycket!!
Jag kom fram till
Ja, det verkar rätt.


