Integral/Area och (-) rektangel
Hej,
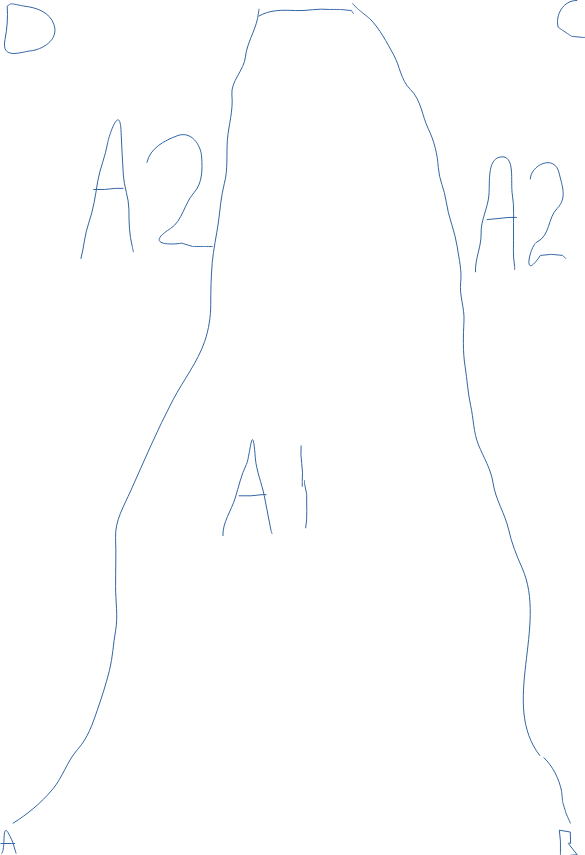
I denna så ska man visa att A1 är dubbelt så stort som A2. Nu när jag kopierade över den så kom inte linjerna runt omkring med. Men ABCD formar således en rektangel runt.
Maxpunkten i grafen (integralen?) tangerar överdelen av rektangeln (CD)
A1= Integral (från A till B väl?)
A2= Rektangel-A1
Hej.
Ser bilden alltså ut så här?

I så fall ska du beräkna integralen av f(x) från vänstra hörnets x-koordinat till högra hörnets x-koordinat. Detta ger dig nämligen arean A1.
Du ska sedan visa att integralens värde är lika med en viss andel av rektangelns area.
Jag lämnar till dig att fundera ut vad denna andel ska vara.
Har du någon funktion för "kurvan" mellan A och B? Givet uppgifterna i din fråga är det inte så lätt att svara.
Har du funderat på att rita dina figurer på papper och lägga upp en bild? Det man ritar på datorn blir inte så bra.
Om kurvan är en parabel så är uppgiften korrekt.
Jo, gjorde det men funkade inte att lägga in den, kunde inte exportera/konvertera till rätt fil, jpn-pg eller vad den heter eller annan fil. Bilden ser ut som Ys bild. Så kurvan är en parabel (väl?)
Vet inte hur man gör. Men försöker att börja för att förstå vad jag,man gör.
A1= Så gör man en primitiv funktion av f(x)= F(b)-F(a)=?
A2= så är arean av en rektangel basen*höjden= b*c- A1?
A1= 2*A2
Henrik 2 skrev:Jo, gjorde det men funkade inte att lägga in den, kunde inte exportera/konvertera till rätt fil, jpn-pg eller vad den heter eller annan fil. Bilden ser ut som Ys bild.
Du behöver inte hålla på och krångla med exporter och konverteringar.
Gör som jag, rita för hand på ett papper, logga in på Pluggakuten med din mbil och använd mobilens kamera för att lägga in bilden här.
Så kurvan är en parabel (väl?)
Det vet vi inte, men vi kan säga att den är det.
Vi kan t.ex. bestämma att
Vet inte hur man gör. Men försöker att börja för att förstå vad jag,man gör.
A1= Så gör man en primitiv funktion av f(x)= F(b)-F(a)=?
A2= så är arean av en rektangel basen*höjden= b*c- A1?
A1= 2*A2
Med får vi nollställena och och att symmetrilinjen ligger vid .
Parabeln och rektangeln ser då ut ungefär så här:

För att beräkna A1 ska du då integrera f(x) från x = 0 till x = 4.
Vet du hur du ska göra det?
Tillägg: 30 maj 2024 16:32
Felritat. Rektangeln ska ha höjden 2.
Jag använder dock sällan kameran på mobilen o vet inte hur man skickar men ska kanske börja med det..:)
Jo, det vet jag nog, man tar o gör en primitiv funktion först o sedan integrerar man med 4 o 0.
Men om man inte har en funktion , utan man har enbart y=f(x) kan man inte inte tolka o beräkna ändå med den infon som finns med bokstäverna och att kurvans maxpunkt tangerar rektangel cd?
Ska man hitta på en egen funktion då för att kunna beräkna som i ditt exempel f(x)=x/2 * (4-x) dvs a=o o b =4= med symmetrilinje på x=2?
Jag integrerar o ser vad jag kommer fram till. Hur fick du fram att y=1?
först en primitiv funktion av f(x)= (x/2) * (4-x)
F(X)= (X2 /2*2)* (4X-?)
Kommer inte ihåg vad primitiv funktion av x är?
Mvh/H
Bör inte uppgiften lösas för en allmän rektangel med basen b och höjden h med en inskriven parabel? Det blir inte så svårt som man ev. kan tro från början.
Jag bara vill få den förklarad så jag förstår hur man gör med den info som jag enbart först gav eller om man ska som Y säger hitta på en funktion för att kunna beräkna o visa att A1 är dubbel så stor
Hur gör man? Y får fortsätta när han har tid o förklara men har någon något annat att ge som förslag?
Mvh/H
Henrik 2 skrev:[...]
Men om man inte har en funktion , utan man har enbart y=f(x) kan man inte inte tolka o beräkna ändå med den infon som finns med bokstäverna och att kurvans maxpunkt tangerar rektangel cd?
Om det är en parabel så ja. Men om det är en godtycklig funktion/graf så nej.
Ska man hitta på en egen funktion då för att kunna beräkna som i ditt exempel f(x)=x/2 * (4-x) dvs a=o o b =4= med symmetrilinje på x=2?
Om du vill. Jag försöker konkretisera och exemplifiera så mycket det går eftersom jagntror att du vill det. Men om du hellre vill att vi beskriver lösningsmetoder mer principiellt och generellt så gör vi gärna det.
Säg till hur du vill ha det.
Jag integrerar o ser vad jag kommer fram till. Hur fick du fram att y=1?
Suck. Jag gjorde fel igen. Det ska vara y = 2.
Henrik 2 skrev:först en primitiv funktion av f(x)= (x/2) * (4-x)
F(X)= (X2 /2*2)* (4X-?)
Kommer inte ihåg vad primitiv funktion av x är?
Mvh/H
Nej, det stämmer inte.
Börja med att skriva om funktionen på standarform, dvs f(x) = 2x-x2/2.
Sedan kan du antiderivera term för term.
Ok, så två olika saker här. Kan du visa hur man löser denna uppgift med enbart den info jag gav i inlägg 1 om det är e parabel.
Men sedan kör vi på med konkretiserig som jag vill för en förståelse om man inte vet/ser att det är e parabel
Ok, så man multiplicerar in 0,5 x i parentesen först o får 2x-x2/2. Sedan gör man en primitiv funktion av den?
Mvh/H
f(x)= 2x-0,5x2
F(X)= X2 -(0,5X3)/3
O sedan ska man integrera,testar.
Mvh/H
Fick det till (16-(2/3) upphöjt till 3 och sedan gjorde jag om 16 till 48/3 så det blev (48/3)-(8/3)=40/3
Henrik 2 skrev:Fick det till (16-(2/3) upphöjt till 3 och sedan gjorde jag om 16 till 48/3 så det blev (48/3)-(8/3)=40/3
Hej T,
Tack, men ditt tänk e lite för komplext för mig, hänger inte med alls i din beräkning, hänger enbart med på att du gär en primitiv funktion till f(x).
Om du förenklar,om det går, o förklarar steg för steg din beräkning o variabler i dem.
Mvh/H
Henrik 2 skrev:Hej T,
Tack, men ditt tänk e lite för komplext för mig, hänger inte med alls i din beräkning, hänger enbart med på att du gär en primitiv funktion till f(x).
Om du förenklar,om det går, o förklarar steg för steg din beräkning o variabler i dem.
Mvh/H
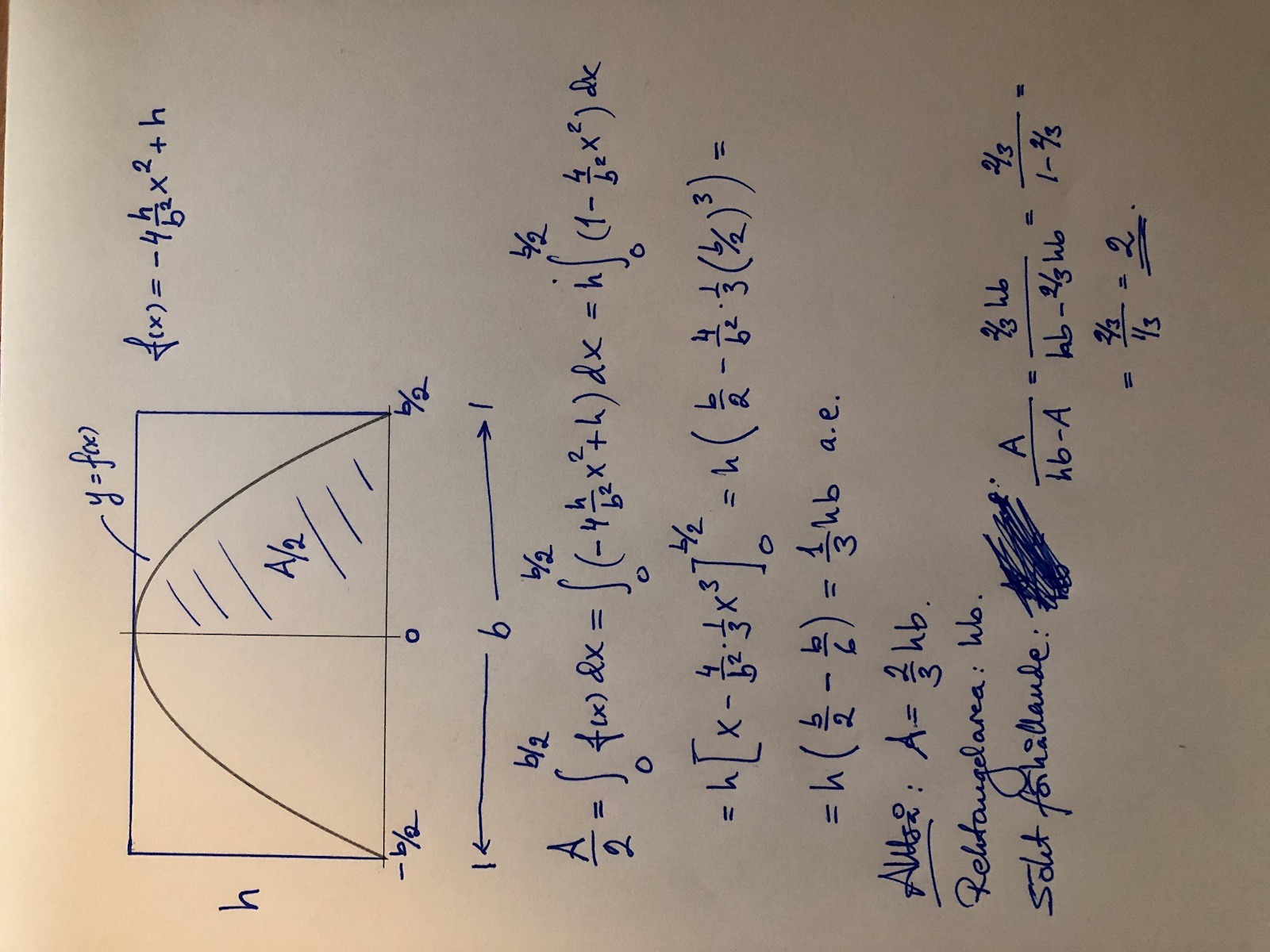
Parabeln har ekvationen
y = -4h/b^2 x^2+h
Då är f(-b/2)=f(b/2)=0 och f(0)=h
Rektangeln har bredden b och höjden h och därmed arean bh.
Istället för att räkna ut arean under parabeln på hela intervallet tar jag [0,b/2] då den är symmetrisk runt origo.
A=hela arean under parabeln. A/2 = integral från 0 till b/2 av f(x) som blir 1/3 bh enligt skissen.
Därmed är hela area under parabeln = 2/3 bh.
Arean inom rektangeln men utanför parabeln är då bh-2/3 bh=1/3 bh
Det sökta förhållandet är därmed ditt "A1/A2" = (2/3 bh)/(1/3 bh) = 2 vilket var det som skulle visas.
Tack T,
Det var bra med ett förtydligande för att försöka hänga med. Ska kika o hoppas på att förstå stegen.
Förklara hur du kommer fram till den funktionen parabeln har. Kan man se/tolka det av hur den ser ut. Du såg min bild,den fula,hehe, i inlägg 1, det ska vara exakt så, eller Ys bild i inlägg 2 e ju precis så det ska vara o man ska utgå från.
Mvh/H
Men då rektangeln har bokstäverna a,b,c o d i sina respektive hörn ska man inte ha med dem i beräkning,formel?
Mvh/H
Henrik 2 skrev:Tack T,
Det var bra med ett förtydligande för att försöka hänga med. Ska kika o hoppas på att förstå stegen.
Förklara hur du kommer fram till den funktionen parabeln har. Kan man se/tolka det av hur den ser ut. Du såg min bild,den fula,hehe, i inlägg 1, det ska vara exakt så, eller Ys bild i inlägg 2 e ju precis så det ska vara o man ska utgå från.
Mvh/H
Med parabeln placerad lämpligt i ett koordinatsystem så att symmetriaxeln är x=0 kommer funktionen ej innehålla en x-term utan vara på formen
Ax^2+B
Då vi vill att höjden skall vara h för x=0 kommer b=h och vi har
Ax^2+h. (1)
Sedan vill vi att (1) skall vara 0 för ±b/2 och får då
A(±b/2)^2+h=0
vilket ger
A=-4h/b^2
och vi har vår slutliga funktion.
Placerar man figuren på annat sätt i koordinatsystemet, likt i Yngves bild, kommer funktionen bli annorlunda, men det gäller att göra det lätt för sig. Oavsett placering blir det samma resultat, men räkningarna kan bli lite mera "grötiga" på väg mot svaret.
Henrik 2 skrev:Men då rektangeln har bokstäverna a,b,c o d i sina respektive hörn ska man inte ha med dem i beräkning,formel?
Mvh/H
Nej, enventuella A, B, C, D är bara för att beskriva en geometrisk figur och har inga värden i beräkningar. Om jag säger att "Mellan Malmö och Stockholm är det 670 km" har Malmö och Stockholm inget värde du kan använda i någon formel. De är endast "ankarpunkter" som hjälper läsaren att förstå hur en bild ser ut och hur den skall tolkas i uppgiftstexten.
Tusan, hade skrivit ett meddelande men datorn e gammal o kraschade, typiskt. Jag e på h(b/2-4/b2 h *1/3(b/2) upphöjt till 3) som i nästa parentes blir h(b/2-b/b.). Kan du förklara enkelt o pedagogiskt hur -4/b2 *1/3(b/2) upphöjt till 3 blir b/b.
I nämnaren så förkortar du med 2 o får kvar b/1 i ena o b/3 o i täljaren så är b=1 så det blir 1/1*1/3 =1/3?
A=1/3 HB + 1/3 HB=2/3 HB,ok.
Rektangels area HB, dvs höjden*bredden eller så kan man lika gärna säga bredden*höjden men du väljer HB här.
Ska kika sökt förhållande..nu..
E så trött så hade inte klarat o förstått detta själv med allt o sedan det sökta förållandet o hur man beräknar, lite för komplext för mig, men ska lära mig det o nöta in det.
Hur får du rektangelns area, hb=1?
Slarvig stil, "b/b" är b/6.
4/b2 *1/3(b/2)^3
=4/b2 *1/3 b^3/8
=1/b2 *1/3 b^3/2
=1/b2 *b^3/6
=b/6
Henrik 2 skrev:E så trött så hade inte klarat o förstått detta själv med allt o sedan det sökta förållandet o hur man beräknar, lite för komplext för mig, men ska lära mig det o nöta in det.
Hur får du rektangelns area, hb=1?
Jag gissar att du menar detta steg
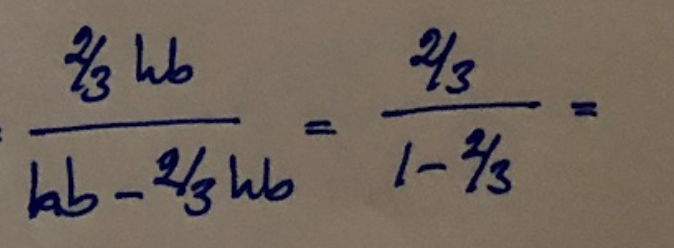
Bryt ut hb från täljare och nämnare och "förkorta bort" hb
Beräknande o förenklade o fick,skönt nog också b/6. så den e ok.
Ja, det steget. Aha, så egentligen e inte hb =1, men iom att hb e både i täljaren o nämnaren så blir det 1 i nämnaren o en osynlig 1 i täljaren.
Jo, men ska nog kunna nöta in detta, kanske. Men om man inte har något mer än den infon som jag gav i inlägg 1 så är det så här man gör. Förstår faktiskt inte fortfarande hur du kommer fram till den funktionen som du gör, men du e ju insatt i matte o kan trolla fram sådant,hehehe..:)
Mvh/H
P.s detta hjälper mig otroligt mycket,hade aldrig kunnat lösa dett själv o komma vidare.



