Integral/Area
Hej,
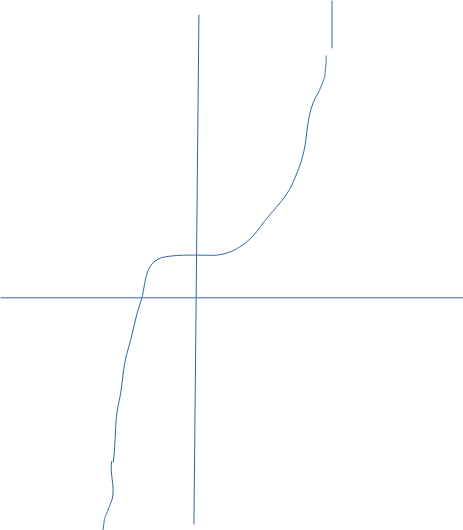
Beräkna arean av grått .
L=Linje=14,5 som är höjden.
f(x)= 0,8x3 +2
Hej.
Om grafen varken skär x-axeln eller linjen y = 14,5 någonstans i intervallet så är ett intuitivt sätt att beräkna Agrått följande:
- Beräkna rektangelns area
- Beräkna Avit med hjälp av en integral
- Subtrahera Avit från rektangelns area
Vet du hur du kan kontrollera huruvida grafen skär x-axeln och/eller y = 14,5 eller inte?
Nja, den går ner till ca 2 på y-axeln men tror väl den ska gå upp till linjen 14,5?
Snabbast är att använda något digitalt grafiskt hjälpmedel som t ex. din grafräknare, Geogebra eller Desmos.
Rita grafen y = 0,8x3+2 och grafen y = 14,5.
Skär de varandrai det aktuella intervallet?
Alternativt lös ekvationen 0,8x3+2 = 14,5.
Ligger lösningen I aktuellt intervall?
f(3) är större än 14,5, hur påverkar det bilden?
Men vad har skärningspunkten med arean att göra.
Vad säger 0,8x3+2 = 14,5?
Jag gjorde så, tog arean av integral dvs 0 till 3 sedan primitiv funktion av 0,8x3 +2o fick efter integrering 22,2 (a.e)
o sedan e arean av rektangeln då b*h= 3*14,5=43,5
43,5-22,2=21,3 (a.e)?
Korrekt?
Mvh/H
Henrik 2 skrev:Men vad har skärningspunkten med arean att göra.
Om grafen till y = f(x) skär linjen y = 14,5 i intervallet [0, 3] så måste du välja en annan metod för att beräkna Agrått
Vad säger 0,8x3+2 = 14,5?
Den ekvationen ger dig skärningspunkterna mellan grafen y = 9,8z3+2 och linjen y = 14,5
Jag gjorde så, tog arean av integral dvs 0 till 3 sedan primitiv funktion av 0,8x3 +2o fick efter integrering 22,2 (a.e)
o sedan e arean av rektangeln då b*h= 3*14,5=43,5
43,5-22,2=21,3 (a.e)?
Korrekt?
Nej, der gäller bara om grafen y = f(x) ligger mellan y = 0 och y = 14,5 i hela intervallet.
Använd ett digitalt ritverktyg, t ex. grafräknare, Geogevra eller Desmos och rita graferna. Ta en bild och lägg upp den här så kan vi resonera vidare.
Ok, så det gör den ju inte,tror att den/integralestartar på y=2 och går upp til linjen 14,5 och sedan då x=3
Så jag börjar med skärning o plottar in det och ser vad skärningspunkt är och sedan får jag mer förklaring för jag vet inte vad jag gör därefter.
Dock går väl integralen, dvs area vit frå 0 till 3 som sagt?
Henrik 2 skrev:Ok, så det gör den ju inte,tror att den/integralestartar på y=2 och går upp til linjen 14,5 och sedan då x=3
Jag förstår inte vad du menar med detta.
Så jag börjar med skärning o plottar in det och ser vad skärningspunkt är och sedan får jag mer förklaring för jag vet inte vad jag gör därefter.
Rita de båda graferna och lägg upp en bild här. Det är dags för dig att ta det steget nu.
Får x=2,5 tror jag att det står som skäringspunkt o y=14,5
O nu?
Me jag plottar, det e enklare, varför tycker du att jag behöver rita,vet inte hur man gör det...
Henrik 2 skrev:Dock går väl integralen, dvs area vit frå 0 till 3 som sagt?
Det ör önnu för tidigt för det. Vi måste först veta hur graferna ser ut. Annars räknar vi bara i blindo.
Henrik 2 skrev:Me jag plottar, det e enklare, varför tycker du att jag behöver rita,vet inte hur man gör det...
Du kan plotta, det är OK.
Det viktiga är att du lägger upp bilden här.
Jag plottade på räknaren o fick som sagt x=2,5 o y=14,5
Vet inte hur jag lägger upp bild från grafräknaren här o varför mear du att det är nödvändigt när jag fått x o y?
Mvh/H
Du kan ta en bild med mobilen och lägga upp här.
Det är nödvändigt att du förstår hur området du ska areaberäkna ser ut.
Annars vet du inte hur du ska utföra beräkningen.
Men displayen e så pass liten på grafräknaren så vet inte hur jag gör det, e det verkligen nödvändigt att jag gör, kan vi inte lösa detta på annat sätt?
Så att jag har fått x=2,5 o y=14,5 som vi visste från början räcker inte,vad ska jag se?
Ritar med kråkfötter hur grafen ser ut, återkommer o lägger in den.
Men förstår inte,vad e det för linjer som skär varandra i/vid x=2,5?
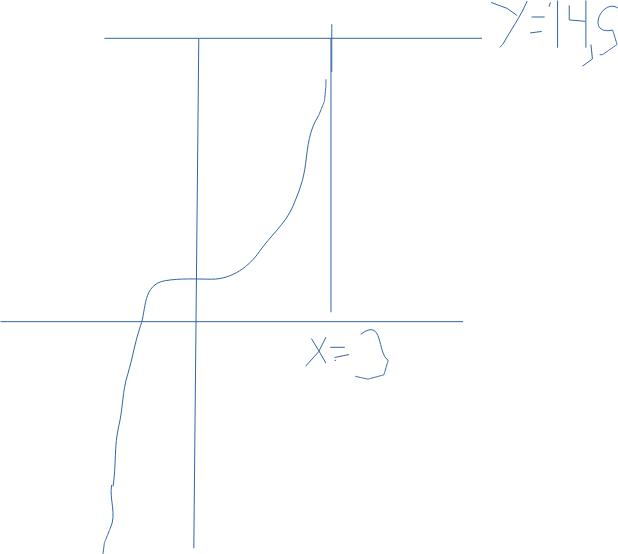
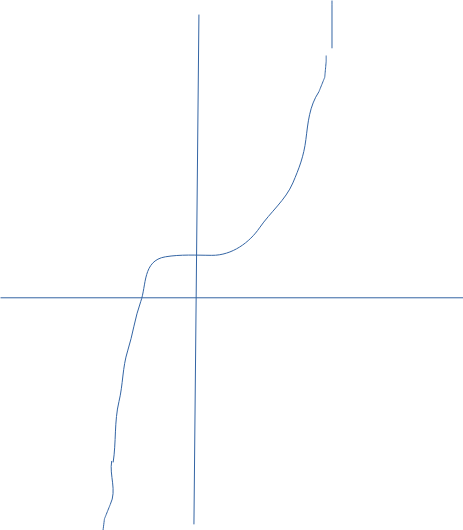
Så här ser grafen ut på ett ungefär, med mina kråkfötter, om jag gjort rätt.
Henrik 2 skrev:Men displayen e så pass liten på grafräknaren så vet inte hur jag gör det, e det verkligen nödvändigt att jag gör, kan vi inte lösa detta på annat sätt?
Jo, du kan berätta hur området ser ut. Men då måste du göra det tydligt.
Förslag: Använd Geogebra eller Desnos istället för grafräknaren.
Så att jag har fått x=2,5 o y=14,5 som vi visste från början räcker inte,vad ska jag se?
Du ska se ich förstå vad det är som begränsar det område du vill areaberäkna. Annars vet du inte hur du ska areaberäkna området.
Ritar med kråkfötter hur grafen ser ut, återkommer o lägger in den.
Men förstår inte,vad e det för linjer som skär varandra i/vid x=2,5?
Det är grafen till y = f(x) och den horisontella linjen y = 14,5.
Henrik 2 skrev:Så här ser grafen ut på ett ungefär, med mina kråkfötter, om jag gjort rätt.
Snyggt. Nu saknar jag bara linjerna y = 14,5 och x = 3.
Det e bilden för skärningspunkt o du ville ha för båda graferna, men det e väl båda då i denna?
Ok f(x) som är =0,8x3 +2 o y=14,5
Denna linje syns inte i bilden då f(x) inte e utritat, än, bara tänker o skriver högt, men nu e den utritad med dess skärningspunkt,ok.
Ska jag rita ut dessa linjer i denna bild o komplettera med?
Men det var ju typ denna som jag hade i inlägg 1?
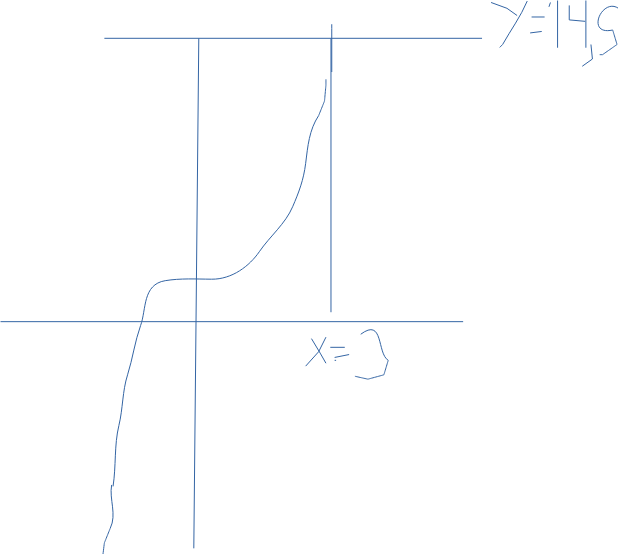
Henrik 2 skrev:Ska jag rita ut dessa linjer i denna bild o komplettera med?
Men det var ju typ denna som jag hade i inlägg 1?
I denna bild ser drt ut som om grafen y = 0,8x3+2 möter linjen y = 14,5 vid x = 3, men så ör inte fallet.
Bilden stämmer alltså inte och riskerar därmed att leda dig fel när du ska beräkna arean.
Använd Geogebra eller Desmos om du tycker att det är svårt att se vad grafräknaren visar.
Ta en screenshot och lägg upp här.
Aha, då e jag med, tack gör om den. Vi får inte ha dessa hjälpmedel på provet, tror jag, så får klara mig utan dessa.
Tror att det var x=3 först i bilden som jag hade satt ut, men linjerna skär varandra innan i x=2,5
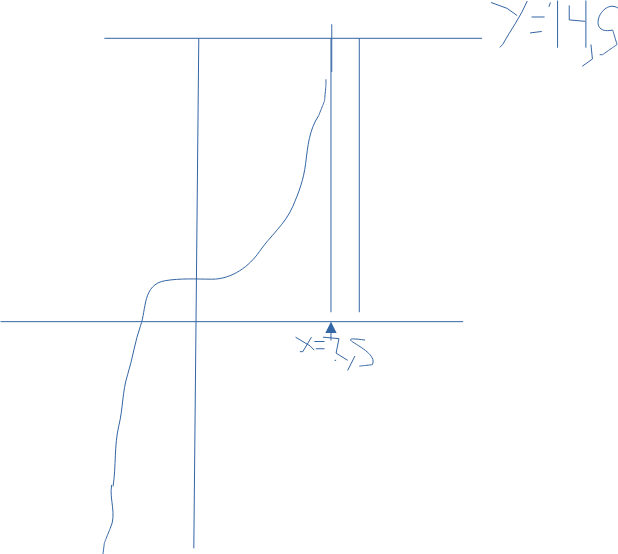
korrigering
Jag gjorde så, tog arean av integral dvs 0 till ,3 sedan primitiv funktion av 0,8x3 +2 o fick efter integrering 22,2 (a.e)
o sedan e arean av rektangeln då b*h= 2,5*14,5= 36,25
36,25-22,2= 14,05 (a.e)?
Korrekt,eller går integralen till 2,5, nu blir jag förvirrad?
Henrik 2 skrev:korrigering
Jag gjorde så, tog arean av integral dvs 0 till ,3 sedan primitiv funktion av 0,8x3 +2 o fick efter integrering 22,2 (a.e)
o sedan e arean av rektangeln då b*h= 2,5*14,5= 36,25
36,25-22,2= 14,05 (a.e)?
Korrekt,eller går integralen till 2,5, nu blir jag förvirrad?
Jag kan ge dig svaret, men det är bättre om du kommer fram till det själv.
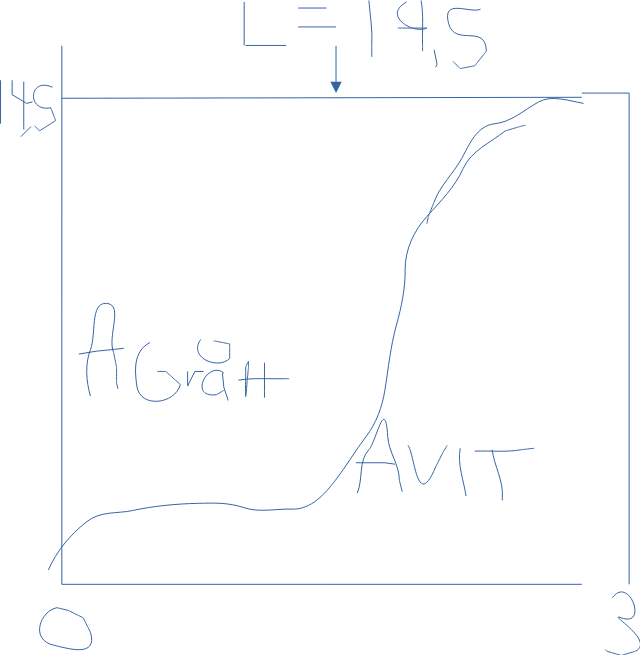
Titta på bilden.
- Är du med på att arean A1 är lika med arean av rektangeln ABCD minus arean av A2?
- Är du med på att arean av A2 kan beräknas med hjälp av en integral?
- Kan du säga vilka koordinater punkterna A, B C och D har, utan att läsa av i bilden?

Jo, dem är väl då (0,0), (0;14,5), (2.5;14,5) och (2.5,0)?
Så man beräknar arean av rektangeln som jag gjorde (?) men integralen går till 2,5 o inte till 3?
Mvh/H
Henrik 2 skrev:Jo, dem är väl då (0,0), (0;14,5), (2.5;14,5) och (2.5,0)?
Ja, det stämmer.
Så man beräknar arean av rektangeln som jag gjorde (?)
Ja, det stämmer.
men integralen går till 2,5 o inte till 3?
Ja, det stämmer.
=======
Förstår du nu varför det är så viktigt att kunna utgå från en hyfsat korrekt skiss över hur graferna förhåller sig till varandra?
Om du kan få den överblicken och förståelsen med hjälp av din grafräknare så är det bra. Annars får du förlita dig på penna och papper om du inte vill/får använda vare sig Geogebra, Desmos eller liknande digitala hjälpmedel.
Ok, jo jag får ta åt mig det o försöka lära mig.
Jag återkommer med beräkningen då.
Får det till 23.4 ca a.e stämmer det?
Om det är 23,4375 du vill avrunda så blir det 23,44.
Henrik 2 skrev:Får det till 23.4 ca a.e stämmer det?
Ja, det stämmer.
Ok, 23,44 med två decimaler.