Integral
Hej,
Innan jag påbörjar denna o integrerar/räknar så undrar jag om den primitiva funktionen är korrekt. 0,5x5 /5 +x?
Det blir plus i o m upphöjt till 4 och det blir x för när man deriverar x så blir det 1 väl?
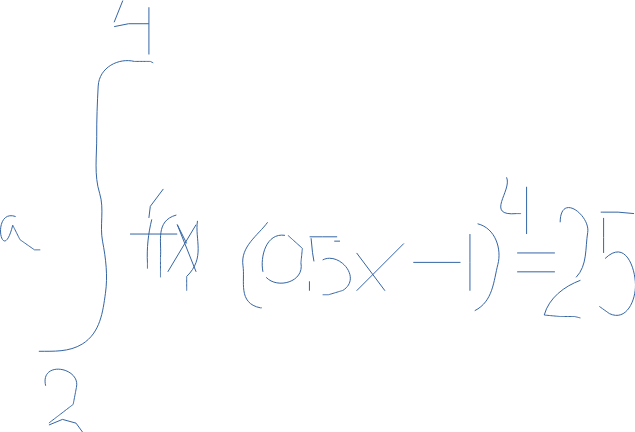
Du kan och bör alltid kontrollera ditt förslag på primitiv funktion.
Derivera ditt förslag och se om du då får tillbaka din ursprungsfunktion.
I så fall var förslaget rätt, annars inte.
Detta följer direkt av att om F'(x) = f(x) så är F(x) en primitiv funktion till f(x).
Lite klurigt när det står så här med en parentes men om det blir utan parentes 0,5x4 +1 är den primitiva väl korrekt?
Mvh/H
Vilken funktion är det du ska integrera?
Är det ?
Eller ?
Det är f(x)= (0,5x-1)4 Men om man tar bort parentesen innan man gör en primitiv funktion blir inte f(x)= 0,5x4 +1? då -1 gånger sig själv jämnt antal gånger blir ett positivit tal.
O sedan gör man en primitiv funktion av denna eller ska man göra utan att ta bort parentesen en primitiv funktion av (0,5x-1)4 o om så hur blir den?
Mvh/H
Sedan så ska det vara a* integralen, glömde att sätta ut*,dvs multiplicerat med integralen.
Henrik 2 skrev:Det är f(x)= (0,5x-1)4 Men om man tar bort parentesen innan man gör en primitiv funktion blir inte f(x)= 0,5x4 +1? då -1 gånger sig själv jämnt antal gånger blir ett positivit tal.
Nej, det gäller inte att (0,5x-1)2 är lika med 0,5x4-14.
Jämför kvadreringsregel, det gäller att (a+b)2 = a2+2ab+b2 och inte a2+b2.
O sedan gör man en primitiv funktion av denna eller ska man göra utan att ta bort parentesen en primitiv funktion av (0,5x-1)4 o om så hur blir den?
Efrersom du läser Matte 3 så antar jag att du inte känner till kedjegrgeln för derivering?
Med hjälp av den kan man nämligen hitta en primitiv funktion till f(x) ganska rättfram.
Ett annat sätt är partiell integration, men det antar jag att du inte heller har stött på.
Om denna uppgift ska lösas med Matte 3-kunskaoer så tror jag att du tyvärr får börja med att utveckla uttrycket till ett polynom av typen ax4+bx3+cx+d och sedan ta fram primitiv funktion till det.
Det blir mycket att skriva, men det går.
Just det ,så e det ju, att jag glömde det, kvadereringsregeln. Blir det då 0,5x4 -2x+1?
Och om så är den primitiva funktionen som skall integreras 0,5x5 /5-x2+(1)x ?
Mvh/H
Henrik 2 skrev:Just det ,så e det ju, att jag glömde det, kvadereringsregeln. Blir det då 0,5x4 -2x+1?
Nej, så enkelt är det inte. Det blir fler termer.
Du kan skriva (0,5x-1)4 som (0,5x-1)2*(0,5x-1)2, utveckla varje parentes för sig och sedam multiplicera ihop parenteserna..
(Eller använda Pascals triangel för att hitta koefficienterna framför varje term )
Kommentar: (0,5x-1)2 är lika med (0,5x)2-2*(0,5x)*1+12.
Parenteser är viktiga.
Nehe, så det gick inte, Pascals triangel har jag inte hört om o lärt mig..:)
Så man måste ta varje parentes för sig o sedan multiplicera ihop dem, då testar jag o ser vad jag kommer fram till.
Mvh/H
Hej,
Puh, nu ska vi se, säkerligen något fel, men here i go:
(0,25x2 -x+1)((0,25x2 -x+1)= 0,25x4 -0,5x3 +0,5x2 -0,5x3 +x2 -x+0,5x2 -x-1=
0.25x4 -x3 +2x2 -2x+1
Primitiv funktion (behövs parenteser runt denna för förståelse) = (0,25x5/5)-(x4/4)+(2x3/3)-(x2)+(x)
Korrekt eller missat något?
Sedan integrera med integrander 4 och 2 och ta vad man får fram o multiplicera det med a=25?
När man integrerar ska man ta 0,25(4)5 , dvs man tar enbart 4an o upphöjer till 5 eller tar man (0,25*4)5 ?
Man ska få a=?
Mvh/H
Vad blir f prim (x)= (0,5x−1) 4?
Mvh/H
Din funktion är f(x) = (0,5x-1)4 =0,0625x4-0,5x3+1,5x2-2x+1. Med den omskrivningen bör det vara genomförbart för dig att derivera den.
Hej S,
Jag tog (0,5x-1)2*(0,5x-1)2= (0,5x2-x+1) *(0,5x2 -x+1)
Sedan fick jag detta till
0,25x4 -0,5x3 +0,5x2 -0,5x3 +x2 -x+0,5x2 -x+1=
0.25x4 -x3 +2x2 -2x+1
Så jag får inte det svaret som du fick av f(x)=(0,5x-1)4 .
Vad gör jag för fel i min beräkning?
Mvh/H
så det blev fel redan där.
Ok, så man kan inte bara lyfta in 2an så det blir 0,5x2 ?
Man ska ta det 0,5x*0,5x så det blir 0,25x2 inom parentesen,ok.
Mvh/H
Förslag:
Börja med att sätta a = 0,5x och b = 1.
Uttrycket blir då (a-b)4, vilket kan skrivas som (a-b)2*(a-b)2.
Utveckla nu kvadraterna var för sig och multiplicera sedan ihop:
(a2-2ab+b2)*(a2-2ab+b2) = a4-2a3b+a2b2 -2a3b+4a2b2-2ab3+a2b2-2ab3+b4 = a4-4a3b+6a2b2-4ab3+b4.
Byt nu tillbaka från a till 0,5x och från b till 1.
Hej,
Men gjorde jag inte så då jag tog (0,5x-1)2*(0,5x-1)2= (0,5x2-x+1) *(0,5x2 -x+1)
Jag lyfte in så det blev 0,5x2 -x+1 och tog inte i den första parentesen 0,5x*0,5x mm som S gjorde som hen då fick till 0,25x2-x+1
(0,5x−1)2 = 0,5x⋅0,5x−1⋅0,5x−1⋅0,5x+(−1)(−1) = 0,25x 2−x+1 )
I den första parentesen är inte detta korrekt (0,5x2-x+1) *(0,5x2 -x+1) eller ska det vara som S säger o som blir ett annorlunda svar än det som jag fick. Jag fick det då sedan mulitplikation med den andra parentesen det till 0,25x 4 o S fick det till 0,0625x4 iom att hen tog 0,25x 2 från den första parentesen:
Henrik 2 skrev:Hej,
Men gjorde jag inte så då jag tog (0,5x-1)2*(0,5x-1)2= (0,5x2-x+1) *(0,5x2 -x+1)
Nej, (0,5x)2 är inte lika med 0,5x2
Jag lyfte in så det blev 0,5x2 -x+1 och tog inte i den första parentesen 0,5x*0,5x mm som S gjorde som hen då fick till 0,25x2-x+1
(0,5x−1)2 = 0,5x⋅0,5x−1⋅0,5x−1⋅0,5x+(−1)(−1) = 0,25x 2−x+1 )
I den första parentesen är inte detta korrekt (0,5x2-x+1) *(0,5x2 -x+1)
Nej, det är inte korrekt. Se nedan förslag om a och b.
eller ska det vara som S säger o som blir ett annorlunda svar än det som jag fick.
Jag fick det då sedan mulitplikation med den andra parentesen det till 0,25x 4 o S fick det till 0,0625x4 iom att hen tog 0,25x 2 från den första parentesen:
Räkna med a och b som jag föreslog istället. Då blir det färre saker att hålla i huvudet och därmed enklare att hålla reda på faktorerna.
Ok, så det blir inte 0,5x2 inom parenteserna utan det blir som S skrev 0,5x*0,5x=0,25x2
Kikar på inlägg 17 o försöker följa det.
Mvh/H
Henrik 2 skrev:
Ok, så det blir inte 0,5x2 inom parenteserna utan det blir som S skrev 0,5x*0,5x=0,25x2
Det stämmer.
Kikar på inlägg 17 o försöker följa det.
Bra.
På samma sätt kan du komma fram till "kuberingsreglerna"
- (a+b)3 = a3+3a2b+3ab2+b3
- (a-b)3 = a3-3a2b+3ab2+b3
Detta är alltså formler som du kan använda på samma sätt som kvadreringsreglerna i ditt formelblad.
Kuberingsreglerna finns på formelbladet, första sidan högst upp tillsmmans med konjugat- och kvadreringsreglerna.
Om jag försöker stoppa in a=0,5x o b=1 så får jag följande:
0,5x4 -2x3 + 3x2 , men vad blir b2 , tar man 3x2 *12 =3x2 eller tar man 3x2 +12 ?
-4ab3 = -2x3 ? b4 =1 ?
Varför tycker du detta e enklare än att jag då bara tar 0,25x2 o bara multiplicerar det med den andra parentsen,e det för att det e så många siffror/nummer att hålla reda på?
Mvh/H
Ok, kikar på det..Just, ser det nu..kuberingsreglerna e där också inte bara kvadereringsreglerna.
Henrik 2 skrev:Om jag försöker stoppa in a=0,5x o b=1 så får jag följande:
0,5x4 -2x3 + 3x2 , men vad blir b2 , tar man 3x2 *12 =3x2 eller tar man 3x2 +12 ?
-4ab3 = -2x3 ? b4 =1 ?
Nej, om a = 0,5x så är a4 = (0,5x)4, vilket är lika med 0,54*x4, vilket är lika med 0,0625x4
Varför tycker du detta e enklare än att jag då bara tar 0,25x2 o bara multiplicerar det med den andra parentsen,e det för att det e så många siffror/nummer att hålla reda på?
Eftersom du gjorde fel tidigare, villet jag tror beror på att du försökte beräkna termerna I huvudet.
Om du fortsätter med a = 0,5x och b = 1 så kan du göra följande "faktaruta" med komponenter från vilken du sedan kan plocka ihop ditt uttryck steg för steg i lugn och ro, utan att behöva hålla reda på så många saker i huvudet samtidigt
- a4 = (0,5x)4 = 0,0625x4
- a3 = (0,5x)3 = 0,53*x3 = 0,125x3
- a2 = (0,5x)2 = 0,52*x2 = 0 25x2
- a = 0,5x
- b4 = 14 = 1
- b3 = 13 = 1
- b2 = 12 = 1
- b = 1
Du får då att
- a4 = 0,0625x4
- a3b = 0,125x3*1 = 0,125x3
- a2b2 = 0,25x2*1 = 0,25x2
- ab3 = 0,5x*1 = 0,5x
- b4 = 1
Hela uttrycket a4-4a3b+6a2b2-4ab3+b4 blir då (plocka från "faktarutan"):
0,0625x4-4*0,125x3+6*0,25x2-4*0,5x+1
Detta kan förenklas till
0,0625x4-0,5x3+1,5x2-2x+1
Hej,
Tackar för steg för stegförklaring som jag behöver för att förstå det.
Då kikar jag på detta.
Mvh/H
Hej,
Har gått igenom o skrivit upp, så får nöta in det för grundförståelse. Men denna e inte så lätt att veta hur man gör om o förenklar med så pass många termer, ligger på c-a nivå skulle jag väl påstå. O kanske då lättare att sätta in a och b istället o sedan byta tillbaka när man räknat ut f(x).
Är F(x)= 0,0625x5/5- 0,5x4/4+1,5x3/3-x2-x?
Sedan integrering med 4 och 2.
Mvh/H
Henrik 2 skrev:[...]
Är F(x)= 0,0625x5/5- 0,5x4/4+1,5x3/3-x2-x?
Läs svar #2 igen och följ tipset där.
Vad kommer du fram till?
Kommer fram till att F(x) är det som jag kom fram till men ville dubbelkolla.
Jag deriverar det och får f(x)?
Mvh/H
Du har skrivit att sista termen I F(x) är -x, men den ska vara +x.
Hej,
Ja, det ser jag nu, men hade skrivit ner + x,. Så skrev den sista termen fel men +x ska det vara.
Så nu e det integrering med integranderna (heter det integrander?)4 och 2 och det talet man får där ska man* med a=25
Så utan att veta talet så blir det a*talet=25
Seda så dividerar man 25 med detta tal så får man ut a.
Är detta korrekt tänkt och man ska ha ut vad a är?
Mvh/H
Henrik 2 skrev:[...],
Så nu e det integrering med integranderna (heter det integrander?)4 och 2 och det talet man får där ska man* med a=25
4 och 2 kallas integrationsgränser.
Integrand är det uttryck du integrerar. I det här fallet är det f(x) som är integranden.
Så utan att veta talet så blir det a*talet=25
Seda så dividerar man 25 med detta tal så får man ut a.
Är detta korrekt tänkt och man ska ha ut vad a är?
Ja, om det är.så uppgiften är formulerad så är det rätt.
Aha, ok, så själva f(x) är integranden och 4 o 2 integrationsgränser, så heter det.
Jo, men kika i inlägg 1 så som jag utformat uppgiften då med a * före integralen, glömde dock att sätta ut * sedan f(x)=25
Då gör o tar man som jag frågade för att få ut a?
Mvh/H
"Bump"
Hur blir det med med integrering av 2 och 6(ta 6 istället för 4) o därefter tar man talet som man kommer fram till *a=25 Dvs a* talet (som man får efter integrering)=25
Man ska få ut a,vad blir a?
Mvh/H
Du har tänkt rätt men skrivit lite fel.
I första inlägget blir det fel när du dels skriver både och efter integraltecknet, dels glömmer att skriva ut .
Det borde stä
eller
Vad gäller själva uppgiften så kan du skriva
Om nu är en primitiv funktion till så får du
Med
får vi
- (om jag har räknat rätt)
Det ger oss , vilket ger oss
Hej Y,
Nej, nu misstolkar du mig, jag var inte tydlig kanske.
Se inlägg 1 igen, men det kanske inte behövs. Jag skulle skrivit där a* integral 2-6 f(x) (0,5x−1)4 dx=25
Vi har redan kommit fram till den primitiva funktionen är F(X)=0,0625X5/5-0,5x4/4+1,5x3/3-x2+x eller med förenkling enligt som du skriver då du delat täljaren med nämnaren men jag lät det stå som det stod.
Denna primitiva funktion ska ha integrationsgränserna 2-6 (övre o undre).Den ska inte ha 0 som undre gräns utan den ska ha 2 som undre gräns. Dessa ska stoppas in i den primitiva funktionen istället för x, som du vet. Dvs a* (F(6)-F(2))=25
Så kan du nu göra om det så jag ser att jag får samma som du. Jag får efter detta 12,8 o vad får du?
Mvh/H
Henrik 2 skrev:Nej, nu misstolkar du mig, jag var inte tydlig kanske.
Se inlägg 1 igen, men det kanske inte behövs. Jag skulle skrivit där a* integral 2-6 f(x) (0,5x−1)4 dx=25
Jag har ringat i rött det som är formellt fel. Det ska stå antingen f(x) eller (0,5x-1)4 efter integraltecknet, inte både och. Det ska stå dx på slutet.

Jag får efter detta 12,8 o vad får du?
Jag får a -0,336.
Om du visar i detalj hur du räknar så kan vi hjälpa dig att hitta feletm
Ok, då tar du bort f(x), iom formellt fel. Det ska självfallet vara det som vi diskuterat o som jag får nöta in med a o b termer o sedan byta tillbaka som du försöker lära mig.
Integrationsgränserna/integralen ska nu vara från 2 till 6, inte 2 till 4, o inte heller 0 till 4 utan det ska vara 2 till 6 , den övre respektive undre gränsen.
Mvh/H
Hej,
F(6)=0,00125⋅65−0,125⋅64+0,5⋅63−62+6=9,72−162+108−36+6=−74,28
Har här fått som du, dock så har du väl fått en 0 för mycket i 0,00125, det ska väl vara 0,0125 och med det så blir det 97,2 och inte 9,72 och då blir F(6)=13,2?
Sedan integrering av 2 fick jag till 0,4 vad får du/ni?
Mvh/H
Ja, det stämmer, jag skrev fel.
Första termen i F(x) ska vara 0,0125*x5.
Då får vi, som du mycket riktigt påpekar:
- F(6) = 13,2
- F(2) = 0,4
Och vi får då a = 25/(13,2-0,4) 1,95
Hej Y,
Yes, precis detta som jag fått, men ville dubbelkolla. Tänkt att jag också räknar rätt ibland o du fel, händer inte ofta ,men även dem bästa gör fel,hehehe..:)
Mvh/H
Hej,
A=0,5x och b är satt till =1
Men i parentesen står det -1 . Blir det 1 för att man upphöjer det till ett jämt antal?
Eller ska b=-1?
Mvh/H
Henrik 2 skrev:[...]
A=0,5x och b är satt till =1
Men i parentesen står det -1 . Blir det 1 för att man upphöjer det till ett jämt antal?
Eller ska b=-1?
Pröva!
Du har uttrycket 0,5x-1 som du vill skriva som a-b istället.
- Hur blir a-b om du väljer a = 0,5x och b = 1?
- Hur blir a-b om du väljer a = 0,5x och b = -1?
Vad drar du för slutsats?
E det för -(-1) som således blir 1?
Eller e det för att man redan har minus framför b, så behövs inte ett minus till?
Ja, det e för att a-b, dvs att man skriver b=1 för man har ,minus framför b redan.
Mvh/H
Henrik 2 skrev:[...]
Ja, det e för att a-b, dvs att man skriver b=1 för man har ,minus framför b redan.
Det stämmer.
Ok.



