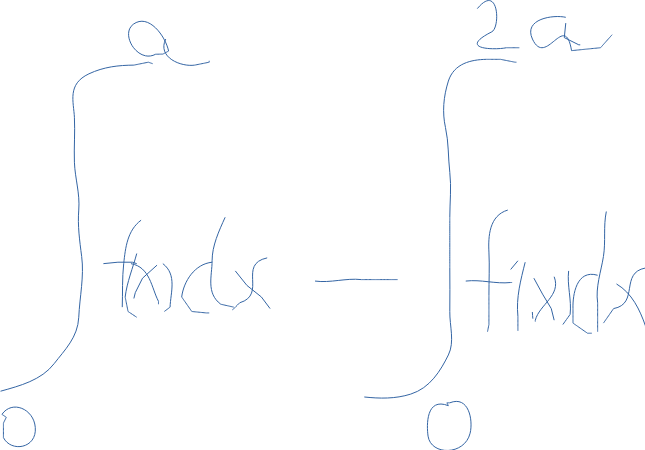
Integral

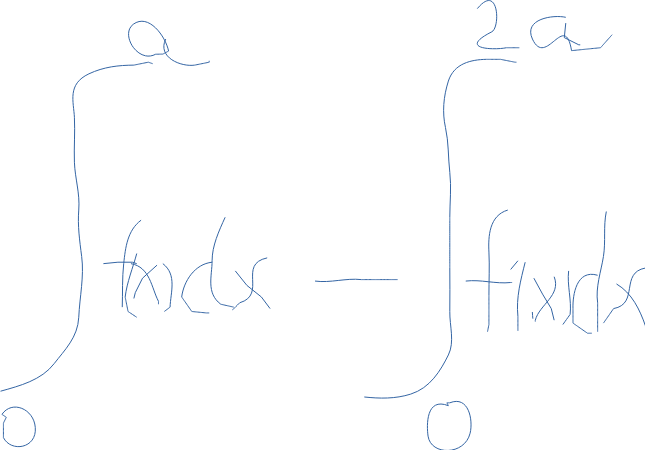
Låt  F  vara en primitiv funktion till  f  .

Då kan den första integralen skrivas   F(a) – F(0)
                                      och den andra    F(2a) – F(0)

Kommer du vidare från det?

Henrik 2 skrev:

Hej,

Man ska göra om dessa två integraler till enbart en integral  där konstanten a$>$0

Förstår inte ,än,hur man tänker. Om ni inte kan se vad det står så är det f(x)dx

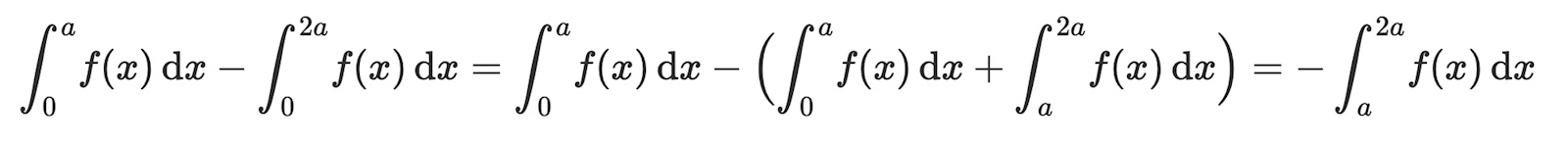
Hej,

Två olika svar.  I de första förklaringen av dig Arktos förstår jag inte blir det a från första integralen-2a från den andra integralen=-a?

Det låter ju inte rimligt då a ska vara större än 0,vs positivt

I Trinitys förklaring förstår jag inte heller riktigt varför man sätter det inom parentes och sedan blir plus?

0 går mot a i den första o sedan i den andra så går 0 mot 2a.

Jag förstår inte detta just nu.

Mvh/H

Om jag förstår dig rätt Henrik. Värdet av F(0) behöver inte vara 0 då a=0. Både Arktos och Trinity försöker beskriva två sätt att utföra substraktionen så att vi förenklar uttrycket.

Enligt en av integrationsreglerna så kan man beskriva ett intervall som innehåller punkterna a, b och c på detta sätt:

${\int }_a^{b}f\left(x\right)dx+{\int }_b^{c}f\left(x\right)dx={\int }_a^{c}f\left(x\right)dx$

Det trinity gjorde var att tillämpa denna regel baklänges för att kunna förenkla uttrycket.

Hej,

Tackar,har inte lärt mig dessa integrationsregler med ett intervall av punkterna a,b o c då jag studerar på distans.

Ok, vet inte om jag förstår det, men man ska inte beräkna något här,utan bara följa dessa regler eller?

Hur kommer man vidare o tänker här?

Jag förstår primitiv funktion av dem båda men inte hur man gör o tänker sedan därefter.

Låt  F  vara en primitiv funktion till  f  .

Då kan den första integralen skrivas   F(a) – F(0)   och den andra    F(2a) – F(0)

Mvh/H

Är du med på att integralerna kan skrivas så? 
Kolla definitionen på bestämd integral

Skillnaden mellan dem blir då

F(a) – F(0)  –  ( F(2a) – F(0) ) = F(a) – F(2a) =  –( F(2a) – F(a))

som är lika med  det sista uttrycket i  #3 (Trinity2)

Ok, vet inte om jag riktigt förstår, men får lära mig det.

Rita figur!
Och kolla definitionen på bestämd integral.
Då SER du, dvs inser hur det hänger ihop.

Rita figur, o kolla definition,sorry men vet inte hur jag ska gå tillväga o hur man gör.

Jag får bara nöta in det, om det går.

Mvh/H

Det du först och främst behöver träna på är att rita grafet - för hand, på rutigt papper. Kommer du ihåg från Ma1 hur man ritar en rät linje omm du vet k-värdet och m-värdet? Kommer du ihåg från Ma2 hur man ritar en andragradsfunktion?

Jo, det ska jag nog göra. Men vad har det med integraler att göra? räta linjens ekvation och dess k o m-värde. O en 2a gradare. Nu gäller det ju integral. Förklara sambandet.

Mvh/H

Ok, e med på att tecknet framför parentsen ändrar tecknet innanför men e inte med logiskt på denna ,men får lära mig dessa integrationsregler som jag inte stött på tidigare.

Mvh/H