inte med i intervall?
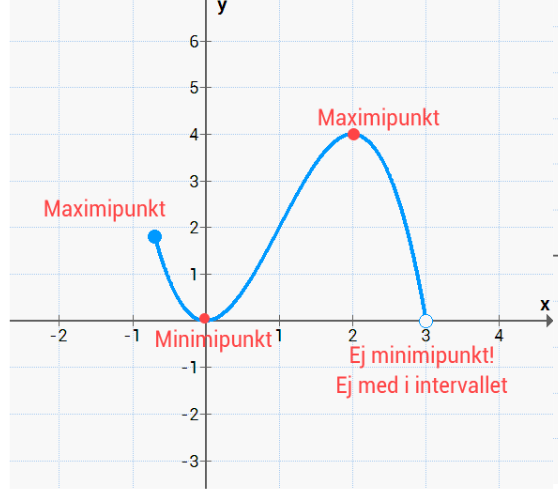
vad menas med att den inte är med i intervallet? varför räknas den inte som minimipunkt? (3,0)
och det här med globala och lokala mini/maxipunkter ... hur avgör man sådant?
är (globala) det största värdet i hela funktionen? och lokala just vid det området?
Jag gissar att det står i uppgiften att definitionsmängden är –1 ≤ x < 3. I så fall finns inget värde för x = 3.
Mogens skrev:Jag gissar att det står i uppgiften att definitionsmängden är –1 ≤ x < 3. I så fall finns inget värde för x = 3.
ingen aning, det var bilden jag mer lade fokus på
https://eddler.se/extrempunkter-extremvarden-och-begreppsroran/
fick den därifrån
kollade igen och det stod såhär:

men det beror på alltså grafens definitionsmängd?
En liten cirkel som inte är ifylld brukar betyda att den punkten inte ingår. En fylld cirkel ingår.
Men det är konstigt om den här bilden inte har någon förklarande text i närheten.
Laguna skrev:En liten cirkel som inte är ifylld brukar betyda att den punkten inte ingår. En fylld cirkel ingår.
Men det är konstigt om den här bilden inte har någon förklarande text i närheten.
Ja..
är en global maxi/minimpunkt alltid även en lokal maxi/minimipunkt?
är en global maxi/minimpunkt alltid även en lokal maxi/minimipunkt?
Ja (men inte tvärtom).



