Inre resistans vs yttre resistans
Gör en uppgift där jag med hjälp av mätdata av spänning och ampere har tagit fram ett diagram som visar lutningen.
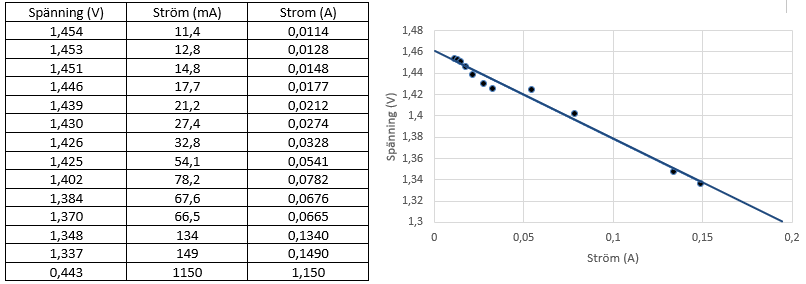
Lutningen på linjen:
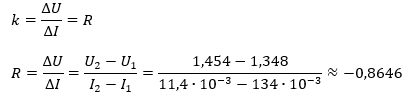
Jag ser att y=kx+m liknar U=-Ri*I+ems men hur kommer det sig att U/I fortfarande blir den inre resistansen Ri och inte den yttre resistansen R? Är det inte det som U/I är?
Ska man räkna ut den inre resistansen så är det väl en annan formel man ska använda?
Kopplingsschemat: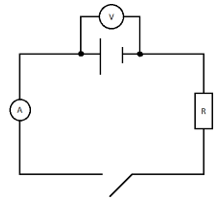
Edit: syftet med uppgiften är att bestämma batteriets inre resistans, Ri , och elektromekaniska spänning, ℰ.
Spänningen i tabellen är mätvärden över spänningskällan. Källan kas ses som en ideal spänningskälla samt en inre resistans.
För att få fram tabellen måste olika yttre resistanser ha använts. Spänningen som ligger över spänningskällan är samma som ligger över R. Det totala motståndet är R + Ri
(EDIT: Förtydligande.)
Ja precis, den yttre resistansen är det som har justerats i testet så att mätvärdena ändras. Enligt uppgiften ska jag bestämma den inre resistansen Ri och den elektromekaniska spänningen, E, men blir inte klok på varför lutningen är -Ri och inte R.
Det beror på var du mäter med voltmetern. Jag ritade in Ri i min bild nedan för att kunna förklara.

Det voltmetern visar är V = U - Ri*I
Det är den räta linjen du ser i ditt diagram.
Så den inre resistansen sjunker när den yttre resistansen minskar? Och eftersom den inre resistansen minskar så ökar strömflödet.
Har varit förvirrande eftersom en lägre spänning vanligtvis har inneburit ett mindre amperevärde.
I ThomasN:s bild är U konstant, den är en ideal spänningskälla. Spänningen i tabell är spänningen över den ideala spänningskällan OCH Ri tillsamman. R varieras för att få fram olika I, annars hade det bara funnits ett (1) mätvärde. Det är olika yttre resistanser som gör att I varierar så mycket i tabellen.
Din mätserie visar alltså hur spänningen ut från spänningskällan varierar med strömmen.
Eftersom den ideala spänningskällan inte variera är enda skillnaden att I*Ri varierar med strömmen (högst rimligt).
Det finns alltså inget som uppenbart antyder att Ri skulle variera med strömmen.
För att göra det tydligare, använd
U=-Ri*I+ems (ems=spänningen för den ideala spänningskällan)
och sätt upp ett ekvationssystem med de två raderna du använde i din beräkning av k.
Räkna ut U och Ri.
Genom att använda beteckningarna från formeln blir det tydligt.
(Lite utanför: Den uppmätta spänningen är samma spänning som den som ligger över yttre resistansen R. Du kan alltså räkna ut vilken yttre resistans R som använts för varje rad i tabellen).
Spänningen U=Ri*I varierar för att den yttre spänningen ändras. Ri är konstant men I ändras vilket ger ett nytt spänningsvärde över spänningskällan.
Ri är alltid 0,8646, dvs konstant.
Är detta korrekt?
Ri är korrekt men troligen inte det du säger om spänngen, inte helt säker på hur du menar.
"Ri är konstant men I ändras vilket ger ett nytt spänningsvärde över spänningskällan" är korrekt.
Spänningen över spänningskällan U=ems-Ri*I
Så man kan inte säga att "U=Ri*I varierar för att den yttre spänningen ändras".
Spänningen från den ideala källan ems är konstant. Dvs spänningen U sjunker då I ökar eftersom spänningsfallet över då Ri ökar.
Löste du ekvationssystemet:
1,454 = ems-Ri*0,014
1,348 = ems-Ri*0,134
Då får du fram värdet på Ri och på den ideala spänningskällan.
Också bra att notera att U=ems då I=0, dvs du får ut vad utspänningen är när källan är obelastad.
Vi har nog fått lite begreppsförvirring här också.
Jag betecknade spänningskällans ems med U i min figur tidigare. Sen har U använts både som spänningen från spänningskällan och spänningen över Ri.
Ja, bra observation. Frågeställaren använde formeln U=-Ri*I+ems i början så jag använde det. Får erkänna att "ems" inte var något jag kan minnas.


