Inlämningsuppgift funktionslära (värdemängd för sammansatt funktion)
Uppgiften lyder:
Låt oss börja med att definiera f:ℝ→]−∞,−1] enligt f(x)=−1/2cos(πx)−2, och g:ℝ→ℝ enligt g(x)=7x/4. I den här inlämningsuppgiften ska vi studera den sammansatta funktionen h av f och g, vilken uppfyller h(x)=f(g(x)) för alla x i dess definitionsmängd.
a) Ge uttrycket för h(x).
- (eget svar)
h(x)=f(g((x))=f(7x4)=−1/2⋅cos(π⋅7x4)−2
h(x)=−cos(π⋅7x4)/2−2
b) Beräkna h(3), h(4) och h(5). Ditt svar ska inte innehålla någon sinus- eller cosinusfunktion och ska inte vara på decimalform.
c) Skriv ut definitionsmängden och målmängden för h.
d) Bestäm värdemängden för h.
e) Är h en injektiv funktion? Om ja, ge ett bevis; om nej, ge ett motexempel.
f) Är h en surjektiv funktion? Om ja, ge ett bevis; om nej, ge ett motexempel.
Jag har löst samtliga uppgifter förutom d). Det jag kommit fram till i d) är att cos(π7x4) kan bara anta värden på intervallet [1,−1] för att vara definierad. Alltså är cos(π7x/4) som mest 1 och som minst −1.
cos(x)=1 då x=2πn för n∈ℤ
Genom att sätta 2πn=π7x/4 får man ett gränsvärde på x då
cos(π7x/4)=1
2πn=π7x/4
2n=7x/4
x=8n/7
Fortsättningsvis är cos(x)=−1 då x=π(2n+1) för n∈ℤ
Genom att sätta π(2n+1)=π7x/4 får man ett undre gränsvärde på x.
π(2n+1)=π7x/4
(2n+1)=7x4
(4/7)(2n+1)=x
x=8n/7+4/7
Sedan har jag provat lite olika värden på n men har inte riktigt lyckats se ett mönster. Det jag kommit fram till är att då cos(x)=-1 måste n vara större än -(4/8).
Då cos(x)=1 måste n vara skilt från 0 samt skilt från -7/8 samt skilt från -4/8
h(x)=−cos(π⋅7x4)/2−2
−cos(π⋅7x4)/2 är som minst -1/2 och som störst 1/2 varför
-5/2 ≤ h(x) ≤ -3/2
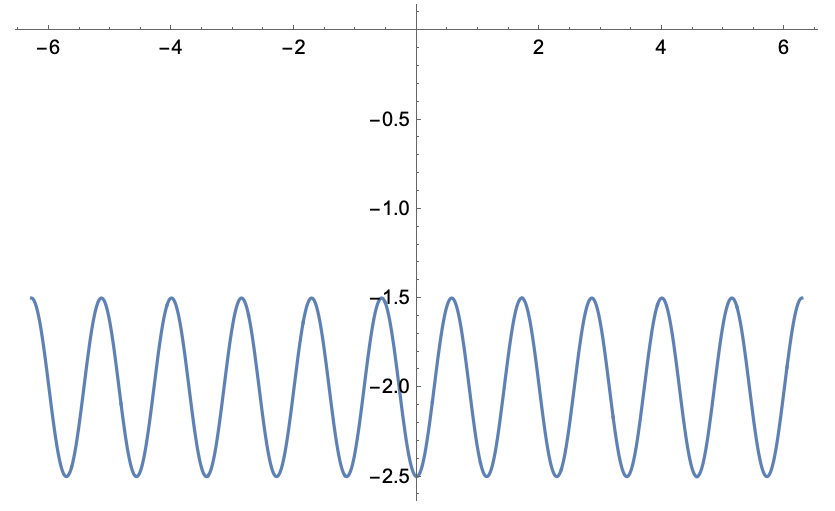
Insåg nu att jag hade missat att lägga till divison när jag kopierade från texten jag hade skrivit i inlämningsuppgiften.
Funktionen är egentligen h(x)=(−cos(π⋅7x/4))/2
Samma princip gäller dock fortfarande antar jag. Tack!

