Injektiv och invers

Frågan lyder:

f(x)= x³+x-9

Visa att f är injektiv och hitta f^-1(x)

Jag kommer fram till att f är injektiv då den är strängt växande. Vilket även derivatan f'(x)=3x^2+1 visar.

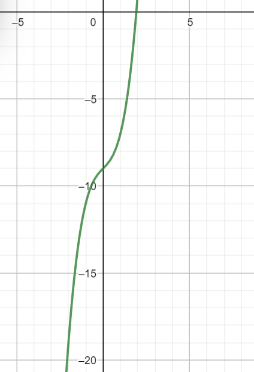
Då f är injektiv ska det finnas en invers

Dock kan jag inte beräkna inversen

y=x³+x-9
x=y³+x-9
x+9=y(y²+1)

Uppfyller funktionen inte något annat krav för att det ska finnas en invers eller gör jag något fel i beräkningen av inversen?

Har du en bild på själva uppgiften. Är du säker att det står hitta f^-1(x)?

Om det står så får man använda digitalmedel då?

Jag ser att jag skrivit fel men jag skulle ändå gjort på samma sätt sökt f^-1(x) för att sedan sätta in 1
Exakt citerat från uppgiften "Let f(x)=x³+x-9. Show that f is injective and find f^-1(1)"

Kan du beräkna $f^{- 1} (1) ?$

Återkom om du behöver hjälp.

Nej då jag skulle gjort likt ovan försökt lösa f^-1(x) vilket jag inte lyckas med kommer endast fram till x+9=y(y²+1) vilket inte är komplett. För att sedan lösa f^-1(1) när jag har inversen. Eller har jag fastnat på något enkelt?

$D u b e h ö v e r i n t e t a r e d a p å f^{- 1} (x) f ö r a t t t a r e d a p å f^{- 1} (1), u \tan d u b e h ö v e r b a r a l ö s a e k v a t i o n e n f (x) = 1$

Okej nu hänger jag med på vad jag tänkt fel på. Kommer då fram till att endast x=2 är en reell rot, blir annars imaginära tal.

Jättebra!

Svara

Visa senaste svar