Induktionsbevis med olikheter - finns det knep?

Nja, den generella metoden är samma oavsett om det är en likhet, olikhet eller något annat. Ibland behöver man använda sig av stark induktion, men det är inte något speciellt för olikheter. Som du säger är det dock ofta egenskaper unika för just det påstående man försöker bevisa som gör att man kommer vidare. Induktion är bara en generell bevismetod och kan se väldigt olika ut. Om du har några exempel på uppgifter så kanske det klarnar lite.

Okej. 

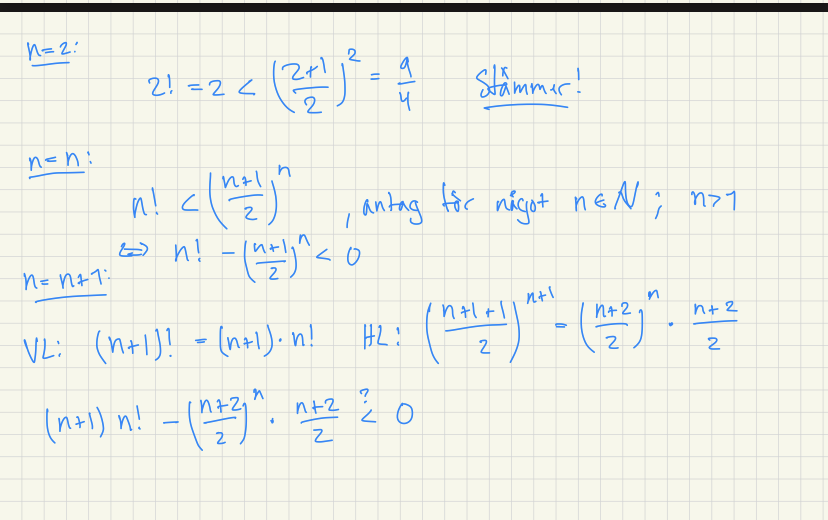(Det kan läggas till att det var länge sedan jag behandlad fakulteter överlag.)

Antar att det har något med faktorerna framför båda faktorererna som vi redan har i induktionsantagandet att göra.

Jag kom på ett direkt bevis.

Låt a+b = k för något fixt k. Vi kan börja med att låta a, b, k vara positiva reella tal Då är produkten a som störst när a = b. Bevis: låt a = k/2 - s, b = k/2 + s. Då är produkten ab = k^2 - s^2. För fixt k är denna produkt maximerad då s = 0.

Betrakta nu produkten n!. Delfaktorerna n*1, (n-1)*2, (n-2)*3,... är parvis mindre än ((n+1)/2)^2 eftersom faktorerna i var och en av dessa har samma summa n+1, och påståendet ovan (modifierat för heltal). Kan du slutföra detta resonemang?

Uppgiften är att lösa med induktionsbevis, men jag kanske kan använda detta. Ska se.

Okej, så här: n!(n+1) <= ((n+1)/2)^n (n+1) = 2((n+1)/2)^(n+1).

Men 2((n+1)/2)^(n+1) <= ((n+2)/2)^(n+1), eftersom

2 <= ((n+2)/(n+1))^(n+1). Kan du visa det?

Jag har ett förslag på ett induktionsbevis. Vi struntar i basfall och induktionsantagande nu, vi antar att vi redan har gjort det. Det vi vill visa är att:

naytte skrev:

Jag har ett förslag på ett induktionsbevis. Vi struntar i basfall och induktionsantagande nu, vi antar att vi redan har gjort det. Det vi vill visa är att:

Lösningsförslag (som förhoppningsvis stämmer, har så lågt blodsocker att handen darrar. Dags att smaska i sig något! :D)

$\displaystyle (k+1)! < \left(\frac{k+2}{2}\right)^{k+1}$ med hjälp av vårt induktionsantagande. Om vi börjar med VL ser vi då att:

$\displaystyle VL = (k+1)! = (k+1)k! < \left(\frac{k+1}{2}\right)^{k}(k+1) =\frac{(k+1)^{k+1}}{2^k}$ enligt induktionssantagandet.

Om vi gångrar båda sidor med en halv ser vi då:

$\displaystyle \frac{1}{2}(k+1)! < (\frac{k+1}{2})^{k+1}$

Detta betyder förstås att om vi har k+2 i täljaren kommer olikheten fortfarande gälla:

$\displaystyle \frac{1}{2}(k+1)! < (\frac{k+2}{2})^{k+1}$

Om vi gångrar med två får vi då:

$\displaystyle (k+1)! < \frac{(k+2)^{k+1}}{2^{k+2}}$

Det följer att om vi gör nämnaren mindre, så blir bråket större. Således:

$\displaystyle (k+1)! < \frac{(k+2)^{k+1}}{2^{k+2}}<\frac{(k+2)^{k+1}}{2^{k+1}}\implies(k+1)!<(\frac{k+2}{2})^{k+1}$

$\blacksquare$

När du multiplicerar båda led med 2 igen så blir nämnaren inte 2^(k+2), utan 2^k.

Attans.

När det handlar om att en summa A_n ska bevisas vara större än nånting B, så kan det fungera bra att betrakta d_n = A_n - B. Den differensen ska då vara positiv och det är ofta så att man kan bevisa att d_n+1 = d_n + nånting positivt.

Man kan också, om vill visa att f(n) < g(n), visa att f(n) < h(n) och att h(n) < g(n). Alltså att man "försvagar" olikheten och visar att den gäller även då. Det är väldigt vanligt att man gör så skulle jag säga.

Jag tackar för tipsen. Vi får se om de räcker, annars är jag snart tillbaka!

Gustor skrev:

Okej, så här: n!(n+1) <= ((n+1)/2)^n (n+1) = 2((n+1)/2)^(n+1).

Men 2((n+1)/2)^(n+1) <= ((n+2)/2)^(n+1), eftersom

2 <= ((n+2)/(n+1))^(n+1). Kan du visa det?

Detta förstår jag. Hur motiverar jag nu att olikheten bara kan vara strikt dvs att de inte kan vara lika?

Tillägg: 25 sep 2024 20:57

Kan jag säga att leden är bara lika då n=0 och eftersom de växer olika fort kommer HL sedan alltid vara större för n>1?

Tillägg: 25 sep 2024 21:02

Alltså den exponentiella tillväxten är snabbare och det är därför det måste gälla?

Enligt induktionsantagandet får vi strikt olikhet: $(n+1)! = (n+1)n! < (n+1){\left(\frac{n+1}{2}\right)}^n=2{\left(\frac{n+1}{2}\right)}^{n+1}$, så om du kan visa att $2\le {\left(\frac{n+2}{n+1}\right)}^{n+1}$ så är du klar, eftersom då är $2{\left(\frac{n+1}{2}\right)}^{n+1}\le {\left(\frac{n+2}{n+1}\right)}^{n+1}{\left(\frac{n+1}{2}\right)}^{n+1}={\left(\frac{n+2}{2}\right)}^{n+1}$, och vi har visat det vi ville. För att visa $2\le {\left(\frac{n+2}{n+1}\right)}^{n+1}$ kan du skriva HL som ${\left(1+\frac{1}{n+1}\right)}^{n+1}$ och använda binomialsatsen. Titta på de två första termerna.

Har inte börjat med binomialsatsen men jag tackar för tipset. Tror jag fick ihop det till slut.

Har samtidigt fått en del tips irl som också fungerade bra. Kan posta de här senare.