Induktion III
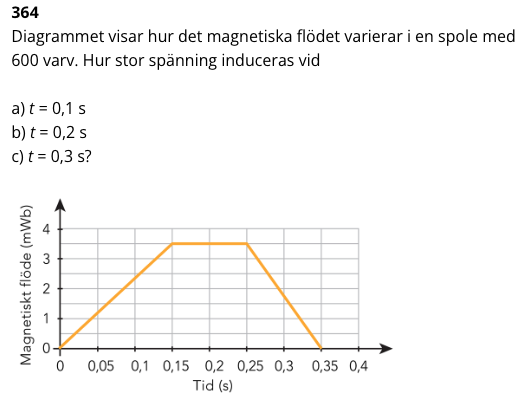
När ska N vara negativt och när ska det vara positivt? i a) ska det vara negativt.
Vad menar du? Minustecknet i formler om inducerad spänning och ström är till för att visa Lenz lag.
Okej men svaret i ex a ska vara negativt, varför?
Hur ser formeln för formeln för inducerad spänning ut?
Inte helt säker på vilken du menar men den jag pratar om som ska verkar va den som ska appliceras i detta exempel är . Det är inte helt klart för mig varför N ska vara negativt eller när.
eddberlu skrev:Det är inte helt klart för mig varför N ska vara negativt eller när.
Det är ett antal (antalet lindningar) som är N. Kan inte vara negativt.
Okej, finns det någon anledning till varför det står såhär då
eddberlu skrev:Okej, finns det någon anledning till varför det står såhär då
Exakt vad jag säger ju.
Men varför skrivs minustecknet ens ut
eddberlu skrev:Men varför skrivs minustecknet ens ut
Det är vad MrPotatohead skrev i #2: för att ange att tecknet (polariteten) ges av Lenz lag.
Den inducerade spänningen i en slinga är
Sedan multiplicera med antalet lindningar.
Aha, oh på vilket sätt ges polariteten av Lenz Lag? så som jag tolkar den så vill den alltid motverka en växlande kraft?
eddberlu skrev:Aha, oh på vilket sätt ges polariteten av Lenz Lag? så som jag tolkar den så vill den alltid motverka en växlande kraft?
Den inducerade spänningen skulle ge en strömriktning som motverkar ändringen av flödet.
Om flödet ökar, är polariteten negativ.
Om flödet minskar, är polariteten positiv.
(Om tecknet är definierat av lindningsriktningen och anslutningar.)




