8
svar
51
visningar
Induktion
Hej,
Hur bevisar jag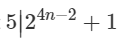 
genom induktion?
Jag har ställ upp så att andra steget lyder:
2^4p-2 +1 = 5k (kan man göra så här?)
och att tredje steget lyder:
2^(4p+2) + 1 = 2^4p * 2^2 + 1, hur kommer jag vidare och får in 2^-2?
2^4p * 2^2 = 2^(4p-2) * 2^4.
Tack, hur går jag vidare härifrån? Nyp att 2^2 fortfarande finns kvar?
Skriv ditt dolda innehåll här
2^4p * 2^2 + 1 = 2^(4p-2) * 2^4 + 1 = (2^(4p-2) + 1) * 2^4 - 2^4 + 1.
Jag hängde inte riktigt med där.
Efter 2^(4p-2) * 2^4 + 1, multiplicerar du in +1? så att det blir 2^(4-2)+1 * 2^4 + 1?
Det kanske blir enklare om du byter ut 2^(4p-2) mot 5k-1.
Ja, men är det tillåtet att göra så? Och är det tillåtet att i andra antagandet konstatera att 2^4p-2 +1 = 5k, där k
Ja, det är ju induktionshypotesen.
ok tack
