Implicita funktionssatsen

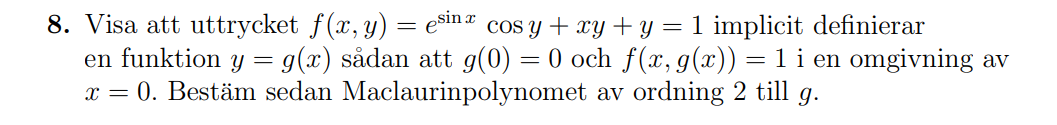
Jag arbetar för nuvarande med denna extenta från 2021 (bild på frågan ovan). Jag förstår principen kring det mesta, och jag kan implicita funktionssatsen. Vad jag inte förstår är hur de kommer fram till denna del av facit (Bild på hela lösningen finns längst ned):

Hur ska man tänka för att komma fram till detta? Såsom jag har förstått det har de deriverat funktionen f(x, g(x)) två gånger med avseende på x, men då får jag en extremt lång ekvation bestående av många cosinus, sinus och e^{sin x}.

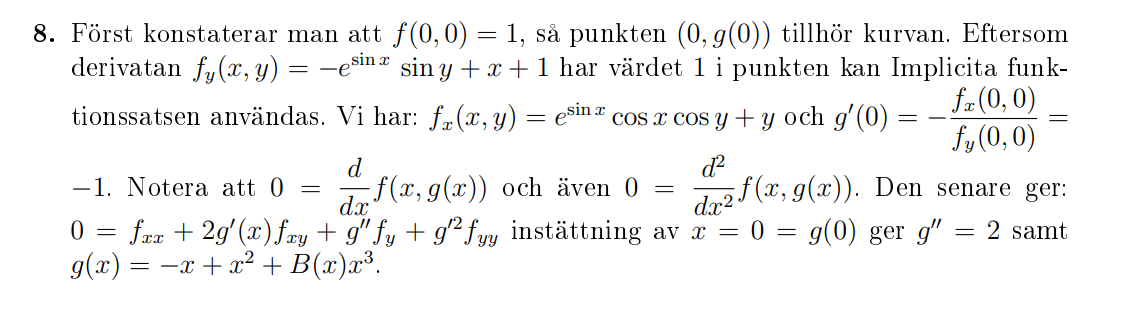
Ja de gör så som du säger. Sedan sätter de in x = 0, utnyttjar att g(0) = 0 och löser ut g’(0) och g’’(0). Maclaurinutvecklingen är g(x) = g(0) + g’(0)x + (1/2)g’’(0)x² + B(x)x³.

Ok! Men hur deriverar man för att komma till just det uttrycket?

Jag tror jag förstår det nu, tack så mycket!

Börja med

$\frac{d}{d x} (f (x, y)) = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \frac{d y}{d x}$ . Där vi ser y som en funktion av x, dvs y = y(x) = g(x).

Sedan fortsätter du på liknade sätt med

$\frac{d}{d x} (\frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \frac{d y}{d x}) = \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} f}{\partial y \partial x} \frac{d y}{d x} + (\frac{\partial^{2} f}{\partial x \partial y} + \frac{\partial^{2} f}{\partial y^{2}} \frac{d y}{d x}) \frac{d y}{d x} + \frac{\partial f}{\partial y} \frac{d^{2} y}{d x^{2}} = . . .$

Svara

Visa senaste svar