Implicit funktion
Jag ställer upp jacobianen och löser ut determinanten men har egentligen ingen förståelse vad det är jag gör, jag följer mer eller mindre algoritmen utantill. Tydligen är det någon transformation från R2 till R3. Bör jag veta något mer?
När det kommer till "Near what points . . ." så förstår jag inte riktigt. Att en funktion är one-to-one betyder det väl att om vi drar en linje parallell med y-axeln så skär denna linje funktionen endast en gång. Kan vi då tänka att vi har en funktion y(ϕ)=R2sinϕ och är inte y one-to-one överallt då? Facit säger annat
Vad gäller inverterbarhet så antar jag att de frågar om själva jacobianmatrisen. Matriser generellt är inverterbara så länge determinanten inte är lika med noll om jag inte minns fel.
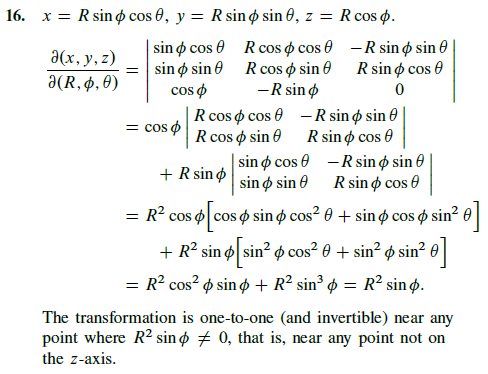
Oj, jag lärde mig använda jakobinen i tidernas begynnelse, jag gladdes åt att den avskräckande determinanten gick att förenkla så långt,
men jag undrar om jag ens i min ungdom Förstod.
Så här får någon kunnigare än jag bidra.
Men en sak, du skriver ”någon transformation från R2 till R3.” Är det inte från R3 till R3 ?
Läs på om inversa funktionssatsen.
PATENTERAMERA skrev:Läs på om inversa funktionssatsen.
Ja, men länken förklarar inte varför determinanten funkar. Man kunde tänka sig en förklaring (jag menar inte bevis) som går ut på att determinanten ger arean av en parallellogram som bestämmer skalfaktorn mellan de gamla och nya koordinaterna – men för många tror jag bara det blir ett hokuspokus som man köper obesett.


