Impedans på rektangulär resp. polär form i en resonanskrets
Hej!
Jag kommer inte vidare på denna uppgiften och skulle behöva lite hjälp. Hur ska jag gå till väga för att få fram värdet på impedansen på polär form? Tar fasförskjutningarna för induktansen och konduktansen ut varandra när de är seriekopplade? Jag tänker att alternativet är att de adderas. Hur ska jag tänka? Beror det på vilken som är kopplad först och sist eller spelar det ingen roll?
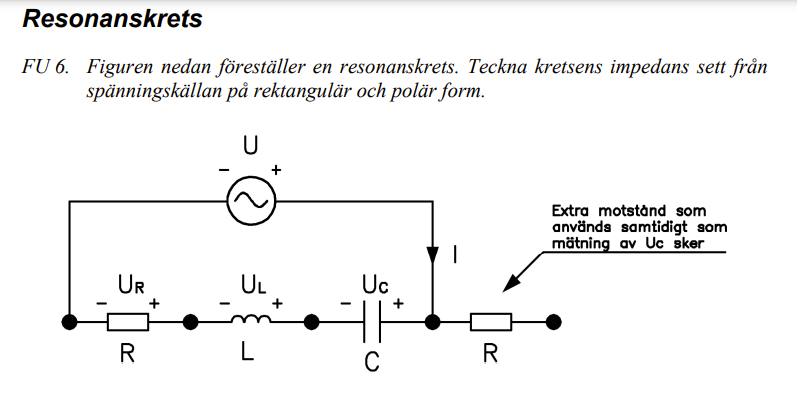
Detta är vad jag fått på impedansen på rektangulär form:

Hej!
Jag tycker du har gjort rätt på den rektangulära formen.
Tar fasförskjutningarna för induktansen och konduktansen ut varandra när de är seriekopplade?
De reaktiva delarna är frekvensberoende som du ser, och tar ut varandra vid resonans.
Beror det på vilken som är kopplad först och sist eller spelar det ingen roll?
Det spelar ingen roll på det matematiska uttrycket, eller hur?
Den polära formen kan du ställa upp ett uttryck för fi och abs(Z) också, eller hur? Med hjälp av L C och R och omega.
Kommer du vidare?
Tillägg: 1 okt 2024 15:33
En sak till. Det heter inte konduktans, det heter kapacitans.
Tack för hjälpen!
Om de tar ut varandra blir fi 180 grader tänker jag. För induktansen ligger spänningen 90grader före strömmen och för kapacitansen ligger spänningen 90 grader efter strömmen. Men hur vet jag att de inte är förskjutna på något annat sätt? Kan det vara för att strömmen genom den och spänningen är samma?
Jag tror att jag har fått fram ett uttryck för absolutbeloppet och vinkeln har jag resonerat mig fram till 180 grader, men känner mig osäker på den. Ska den också vara ett uttryck med omega? Jag har bollat lite men lyckas bara få fram uttryck för frekvensen vilket jag inte kommer vidare med.


Alla komponenterna är seriekopplade, dvs samma ström flyter genom dem (samma fas och storlek). Så alla delspänningar relaterar till den gemensamma strömmen, men delspänningarna blir fasförskjutna inbördes varandra pga den fasvridande impedansen i varje komponent. R'et fasvrider inte strömmen. wL fasvrider 90 grader (spänning före ström), och 1/(wC) fasvrider -90 grader (spänning efter ström). Det betyder att impedansen kan vrida från -90 till 90 grader.
Så fi kommer att bli en funktion av vinkelfrekvensen. Vid resonans, när de reaktiva komponenterna tar ut varandra, får man bara kvar resistansen R i totala impedansen. Och den fasvrider ju 0 grader.
Abs(Z) gör du lite fel på. Titta på min figur, hur borde den bli?

Jag förstår att jag har gjort fel på abs(Z) nu när jag ser din bild, tack för hjälpen! Det borde bli såhär då:

Från din figur kan jag se att ett uttryck borde vara . Stämmer detta? Jag tog ej med j i mitt uttryck då jag tänker att det handlar om triangelns sidors längd, är det korrekt att utelämna det?
Aorta skrev:Jag förstår att jag har gjort fel på abs(Z) nu när jag ser din bild, tack för hjälpen! Det borde bli såhär då:
Ja precis! Nu ser du också att impedansen blir minimal ( och strömmen maximal) vid resonansvillkoret .
Från din figur kan jag se att ett uttryck borde vara φ=arctanϖL-1ϖCR. Stämmer detta? Jag tog ej med j i mitt uttryck då jag tänker att det handlar om triangelns sidors längd, är det korrekt att utelämna det?
Ja det stämmer (skrivs utan tak, jag gjorde en kludd med bläckpenna som gjorde att det såg ut som ett tak). Då ser man att fasen varierar från -90 grader om C dominant och låg frekvens, till +90 grader om L dominant och hög frekvens. Fasvridning 0 grader om det varken finns L eller C i kretsen, eller om kretsen befinner sig i resonans.
Ja precis, utelämna j'et i triangeln. My bad.
Nu är jag med! Tack så mycket för hjälpen!


