Idenrifiera ytor i R3
Jag har svårt att idenrifiera ytor i R3. Det finns olika varianter av ytor. Det jag vill lära mig är strategin (om det nu finns) att identifiera ytan.
Säg att vi x^2+y^2+z^2=1, denna är ellipsoid (deb enda jag kan utan till.
Men om vi har samma ekvation fast en term negativ istället, eller två termer negativa istället, eller att ekvationen =0. Hur ska man tänka där?
Tack på förhand!
Om det är en strategi eller inte vet jag inte, men ett sätt att identifiera ytor kan vara att prova sätta någon term till noll (eller ett annat givet värde). Exempel: x2-y2-z2=1. Vad händer då z = 0, dvs. i xy-planet? Då har vi x2-y2=1, en hyperbel. Det kan vi rita in i vår skiss (jag håller mig till höger om z-axeln, så att skissen blir mindre rörig):
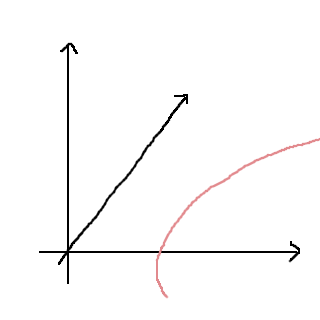
Vad händer nu om y = 0, dvs. Vad händer i xz-planet? Vi kommer att få x2-z2=1, vilket också är en hyperbel. Låt oss rita in den också:
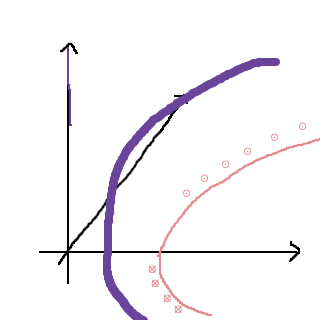
Slutligen, vad händer i yz-planet? -y2-z2=1⇔y2+z2=-1 vilket ger oss en cirkel med radien -1. Ingenting i yz-planet, med andra ord. Summa summarum är att vi tycks ha någon slags hyperbel, fast tredimensionell:
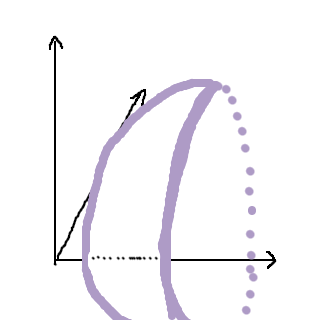
Vi kan kika på hur bra vår gissning är genom att använda exempelvis geogebra:

Vi har lyckats ganska bra!
Kan du göra något liknande för den figur som uppstår då x2+y2-z2=1?
Tack så mycket Smutstvätt! Jag fick till det! Gillade strategin! :)
Vad roligt! Det funkar inte alltid, men det brukar ge en ungefärlig bild av situationen. Det är alltid värt ett försök åtminstone. :)
I vilka fall funkar den inte? Menar du när vi har HL =0?
Det kan nog fungera då HL = 0, jag menar snarare om funktionen är extremt komplicerad. Funktionen f(x,y)=x3√y-x3 ser ut såhär:
Det blir nog svårt att fånga det beteendet genom att bara testa några värden. :)



