I vilket intervall ligger x ?
Förstår inte hur man skulle kunna tänka under tidspress eller hitta nått samband på denna
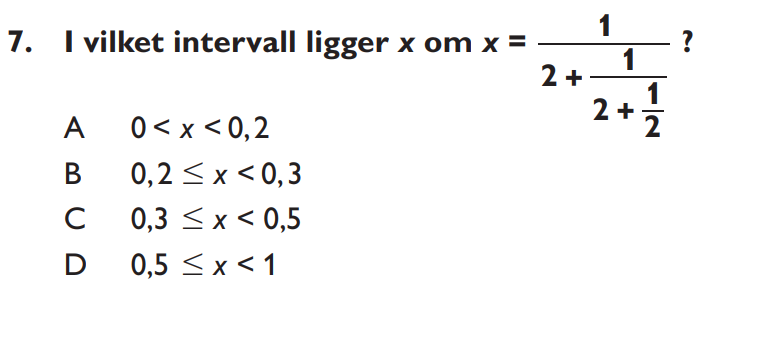
Börja med att bara räkna ut själva uttrycket.
Ör C rätt ?
Arup skrev:Ör C rätt ?
Ja.
Shkan kan du visa hur du skulle löst uppgiften ?
Spontant känns det svårt att undvika att faktiskt räkna ut vad x är, åtminstone i bråkform. Och för att göra det får man nog gå över till gemensam nämnare. Börja med 2+1/2=4/2+1/2=5/2, och 1/(5/2)=2/5.
Sedan kan vi räkna 2 + 2/5 = 10/5+2/5 = 12/5. Och 1/(12/5) = 5/12.
Detta är kanske inte helt lätt att se vad det blir exakt i decimalform, men man kan lätt konstatera att det är mindre än 6/12 = 0,5. Det är också större än 4/12 = 1/3 = 0.33. Så därför kan vi säga att 0.33<x<0.5 och därför är C rätt
Hondel skrev:Spontant känns det svårt att undvika att faktiskt räkna ut vad x är, åtminstone i bråkform. Och för att göra det får man nog gå över till gemensam nämnare. Börja med 2+1/2=4/2+1/2=5/2, och 1/(5/2)=2/5.
Sedan kan vi räkna 2 + 2/5 = 10/5+2/5 = 12/5. Och 1/(12/5) = 5/12.
Detta är kanske inte helt lätt att se vad det blir exakt i decimalform, men man kan lätt konstatera att det är mindre än 6/12 = 0,5. Det är också större än 4/12 = 1/3 = 0.33. Så därför kan vi säga att 0.33<x<0.5 och därför är C rätt
Vad jag tänkte bara var att, 1/(2+1/2) blir ju bara 1/2.5, vilket vi kan förlänga och få att det blir 0.4. 2+0.4 ger 2.4, vilket vi kan räkna ut ganska snabbt att det blir ungefär 0.4 (1/2.5 ger 0.4). Man måste bara ha snabb huvudräkning.
Man får väl använda papper och penna?
En genväg man kan tro på är att talet är 1 delat med nånting som är mellan 2 och 3.
shkan skrev:Hondel skrev:Spontant känns det svårt att undvika att faktiskt räkna ut vad x är, åtminstone i bråkform. Och för att göra det får man nog gå över till gemensam nämnare. Börja med 2+1/2=4/2+1/2=5/2, och 1/(5/2)=2/5.
Sedan kan vi räkna 2 + 2/5 = 10/5+2/5 = 12/5. Och 1/(12/5) = 5/12.
Detta är kanske inte helt lätt att se vad det blir exakt i decimalform, men man kan lätt konstatera att det är mindre än 6/12 = 0,5. Det är också större än 4/12 = 1/3 = 0.33. Så därför kan vi säga att 0.33<x<0.5 och därför är C rätt
Vad jag tänkte bara var att, 1/(2+1/2) blir ju bara 1/2.5, vilket vi kan förlänga och få att det blir 0.4. 2+0.4 ger 2.4, vilket vi kan räkna ut ganska snabbt att det blir ungefär 0.4 (1/2.5 ger 0.4). Man måste bara ha snabb huvudräkning.
Det funkar ju också, men jag skulle nog ha försäkrat mig om att man hamnat i rätt intervall genom att konstatera att 1/2.4 är mellan 1/3 och 1/2 alltså mellan 0.33 och 0.5. (Gör man en för grov uppskattning i vad talet borde vara så finns inga garantier att man hamnar rätt, exempelvis om intervallen är ganska små kanske man approximerar lite för mycket och hamnar fel. Kanske inte någon risk i detta fall eller i de lite tillrättalagda uppgifterna på HP, men ändå, kan vara en skön koll att göra)
Om man tänker sig att kedjebråket fortsätter i oändlighet så gäller att 1/x = 2+x, och det har den positiva lösningen .
Jag tänkte så här (vilket hondel också tycks ha gjort):


