I vilket intervall ligger f(7)
Jag kommer ingenstans med denna uppgift:
Funktionen f har följande egenskaper:
• f(5) = 10,2
• i intervallet 5 ≤ x ≤ 7 gäller att
0,3≤f’(x)≤ 0,8
I vilket intervall ligger f(7)?
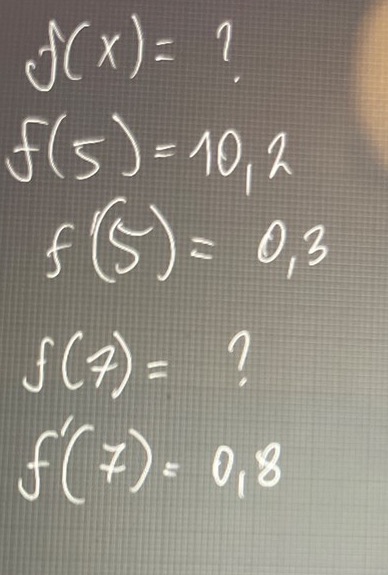
Derivatan innebär förändringshastigheten som är inom ett positivt intervall. Alltså ökar funktionen hela tiden. Hur mycket vet vi inte, men vi kan ta fram ett intervall där f(7) måste finnas.
Undersök vad f(7) blir om funktionen ökar maximalt/minimalt under intervallet.
Tack så mycket! 
Snyggt!
Behöver hjälp med samma uppgift, men fattar verkligen inte vad det innebär att f(7)=10,8 0,3 per x?
Funktionen har värdet 10,8 vid x=7 om derivatan är så låg den kan bli det intervallet, alltså 0,3.
Att derivatan av en funktion har ett värde som exempelvis 0,3 innebär att funktionen förändras med 0,3 för varje steg i x-led. Eftersom vi vill få ut den den minsta möjliga gränsen så antar vi att derivatan är så liten som möjligt i hela intervallet från 5 till 7. Om den ökar med 0,3 per x och går från 5 till 7 alltså 2 steg i x-led måste det minsta värdet funktionen kan anta i f(7) vara 10,2+0,3*2=10,8.
Hänger du med eller blev det rörigt?



